什么是聚类？

使用场景

算法解析

聚类算法

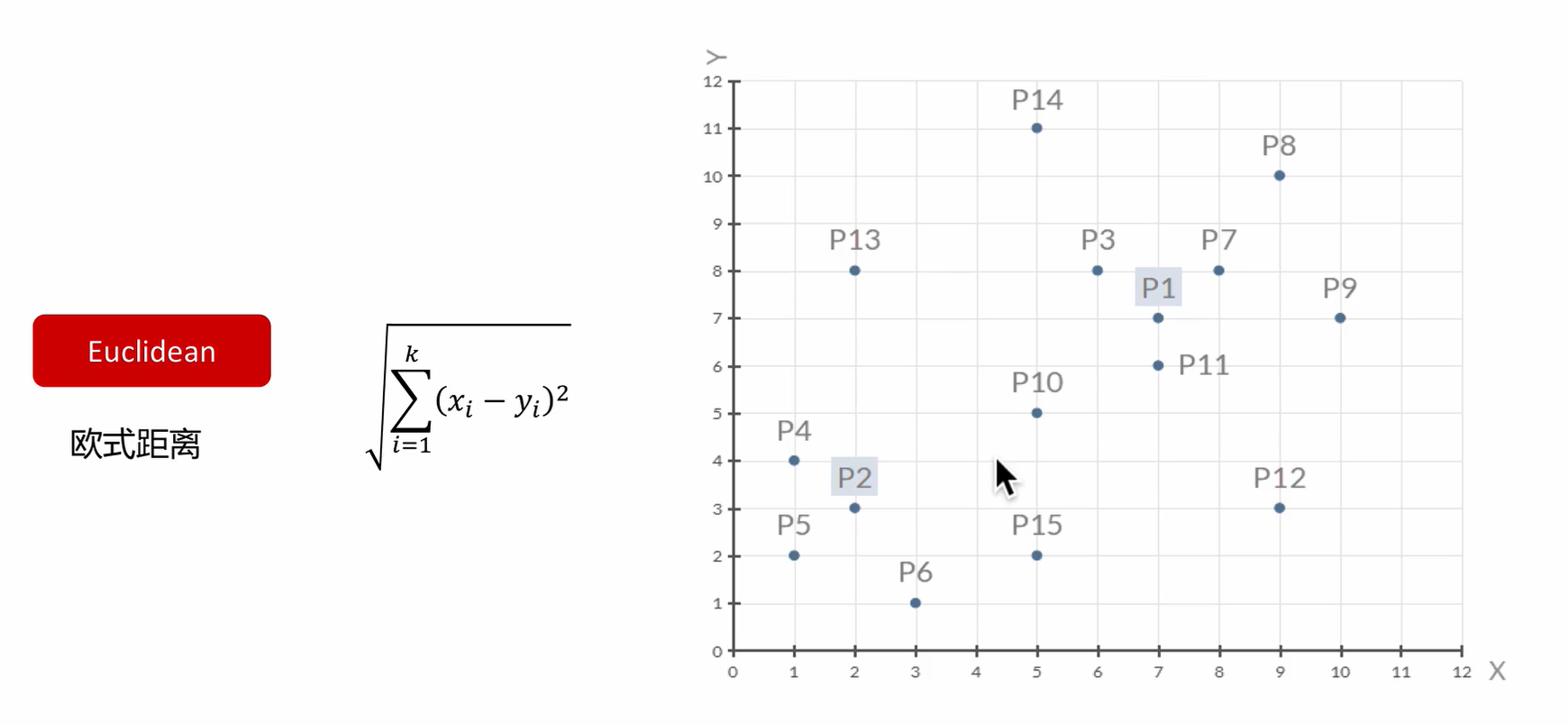
一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

聚类算法与分类算法最大的区别

聚类算法是无监督的学习算法，而分类算法属于监督的学习算法。

  • 无监督：无标签
  • 有监督：有标签

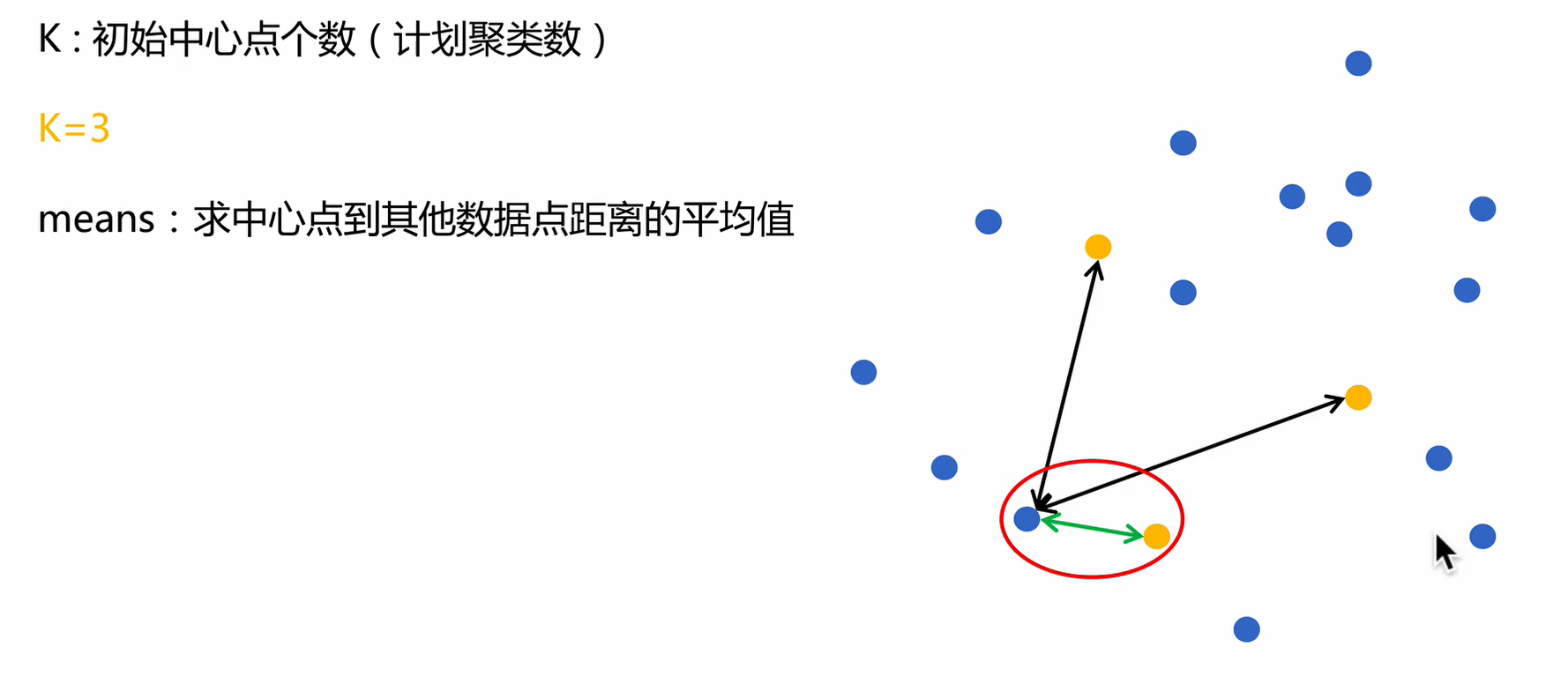
K-Means

K-Means算法接受一个参数K，表示将数据集中的数据分成K个聚类。在同一个聚类中，数据的相似度较高；而不同聚类的数据相似度较低。K-Means算法的步骤为：

  • 步骤一：选择任意K个数据，作为各个聚类的质心，（质心也可以理解为中心的意思），执行步骤二。
  • 步骤二：对每个样本进行分类，将样本划分到最近的质心所在的类别，执行步骤三。
  • 步骤三：取各个聚类的中心点作为新的质心，执行步骤二进行迭代。

迭代的结束条件

  • 当新的迭代后的聚类结果没有发生变化。
  • 当迭代次数达到预设的值。

流程

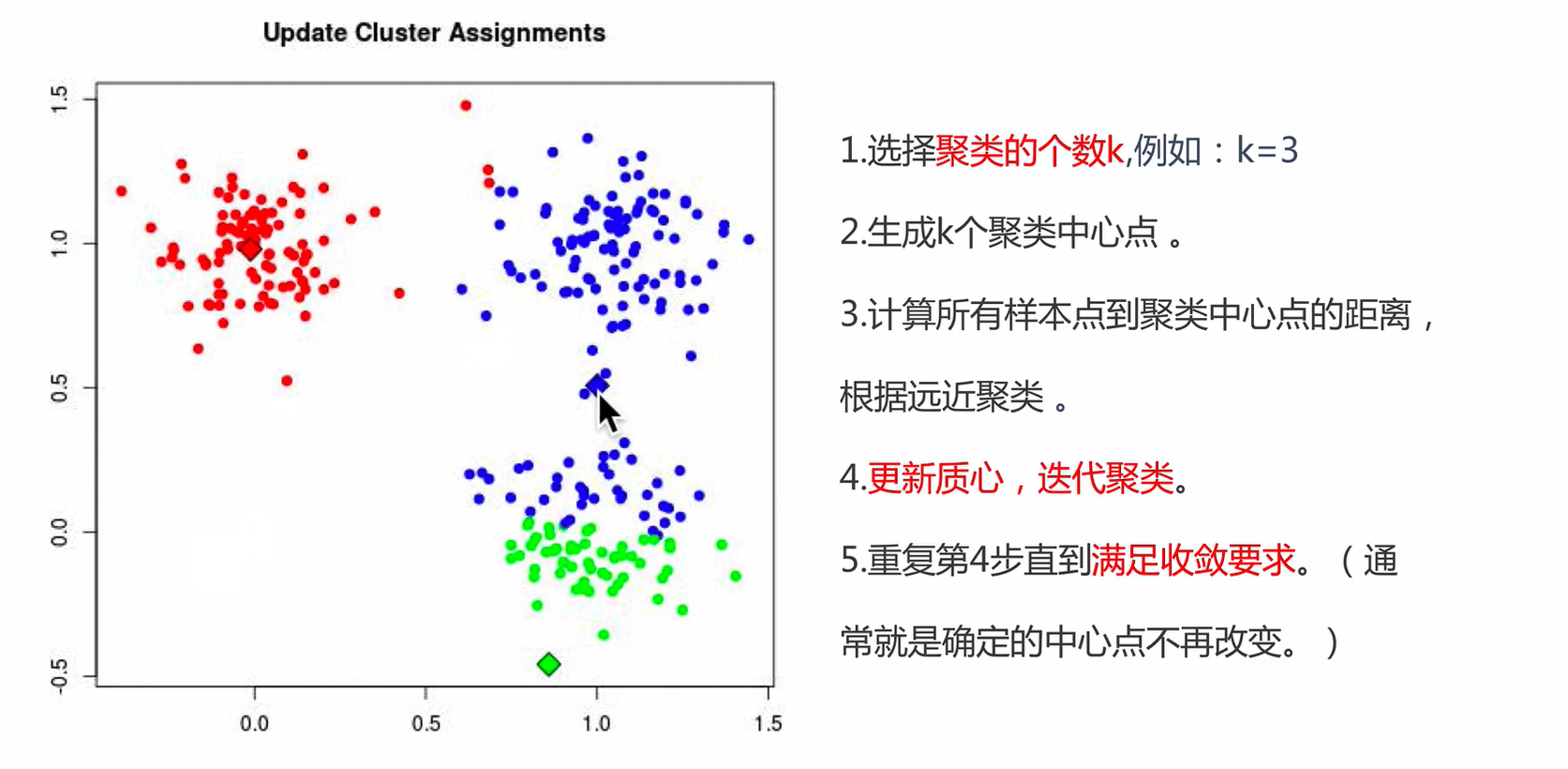
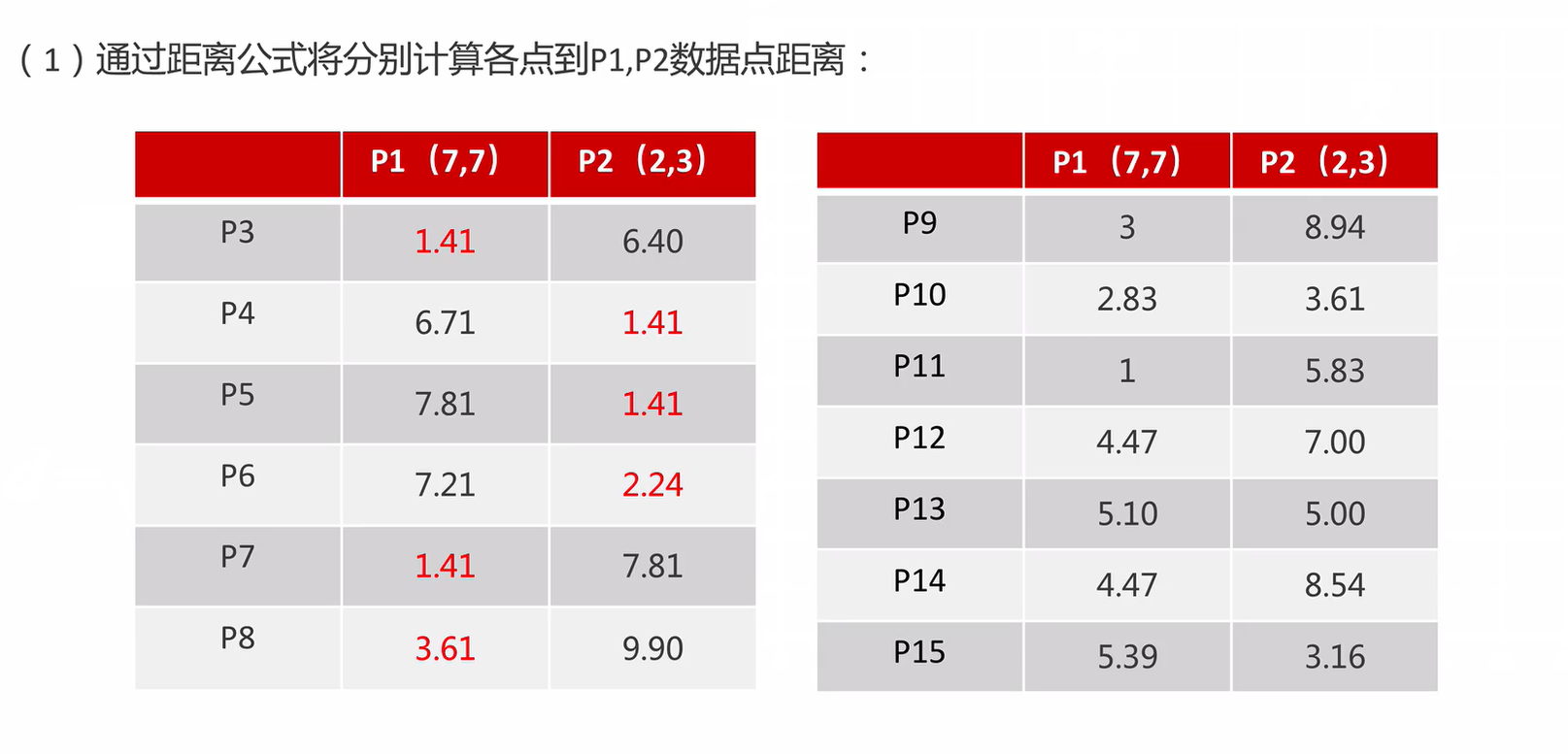
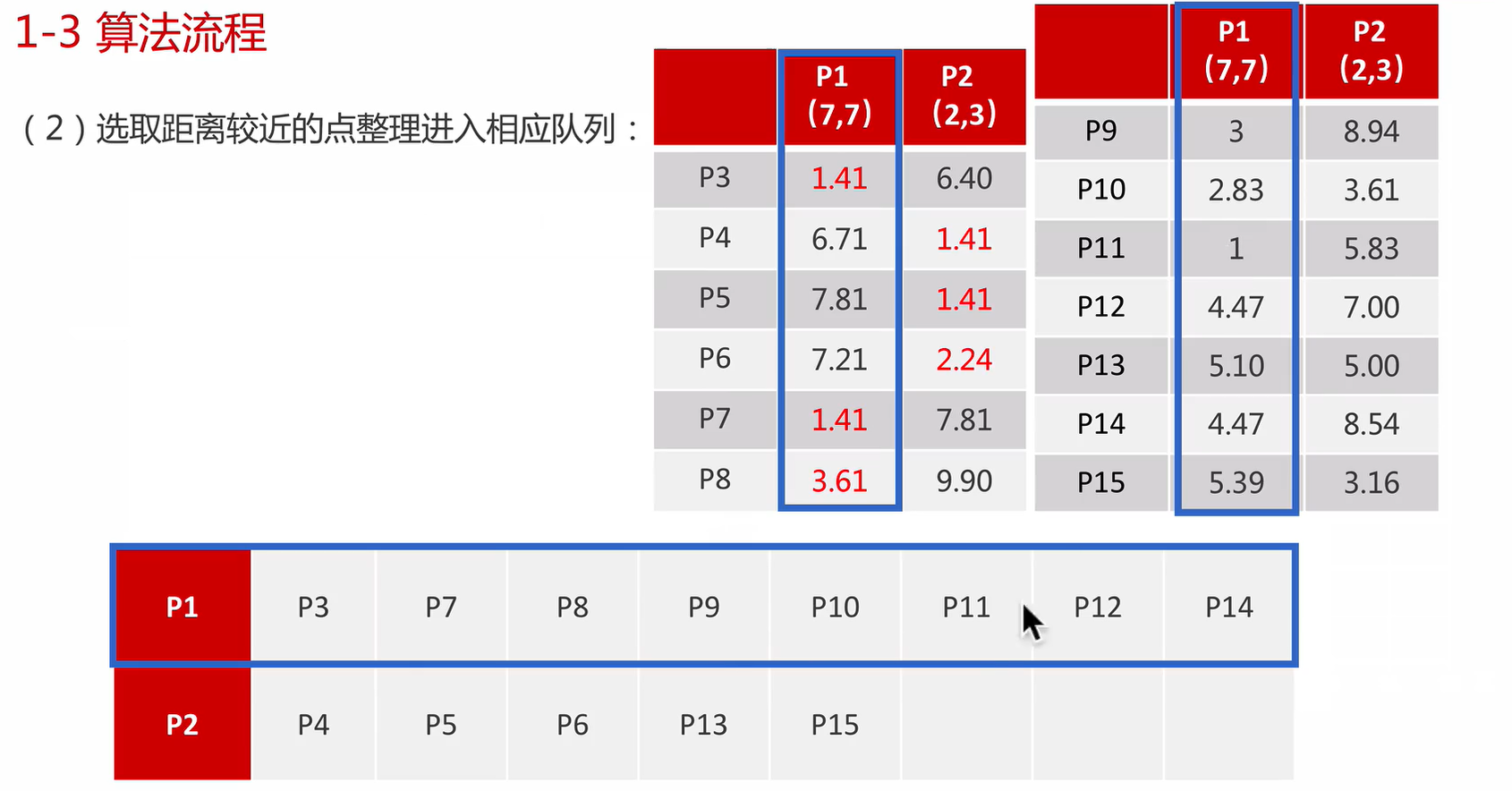
作为新质心，重新聚类，一次上述流程。

收敛：

  1. 设置指定迭代次数。
  2. 当质心变化微乎其微时。

由于每次都要计算所有样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。

测试

代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.datasets import make_blobs

# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本4个特征，共4个簇，簇中心在[-1,-1], [0,0], [1,1], [2,2]， 簇方差分别为[0.4, 0.2, 0.2]
X, Y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.2, 0.2, 0.2],
                  random_state=9)
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()

from sklearn.cluster import KMeans

y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

# 用Calinski-Harabasz Index评估的聚类分数

print(metrics.calinski_harabasz_score(X, y_pred))

from sklearn.cluster import KMeans

y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

print(metrics.calinski_harabasz_score(X, y_pred))

from sklearn.cluster import KMeans

y_pred = KMeans(n_clusters=4, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

print(metrics.calinski_harabasz_score(X, y_pred))

结果：

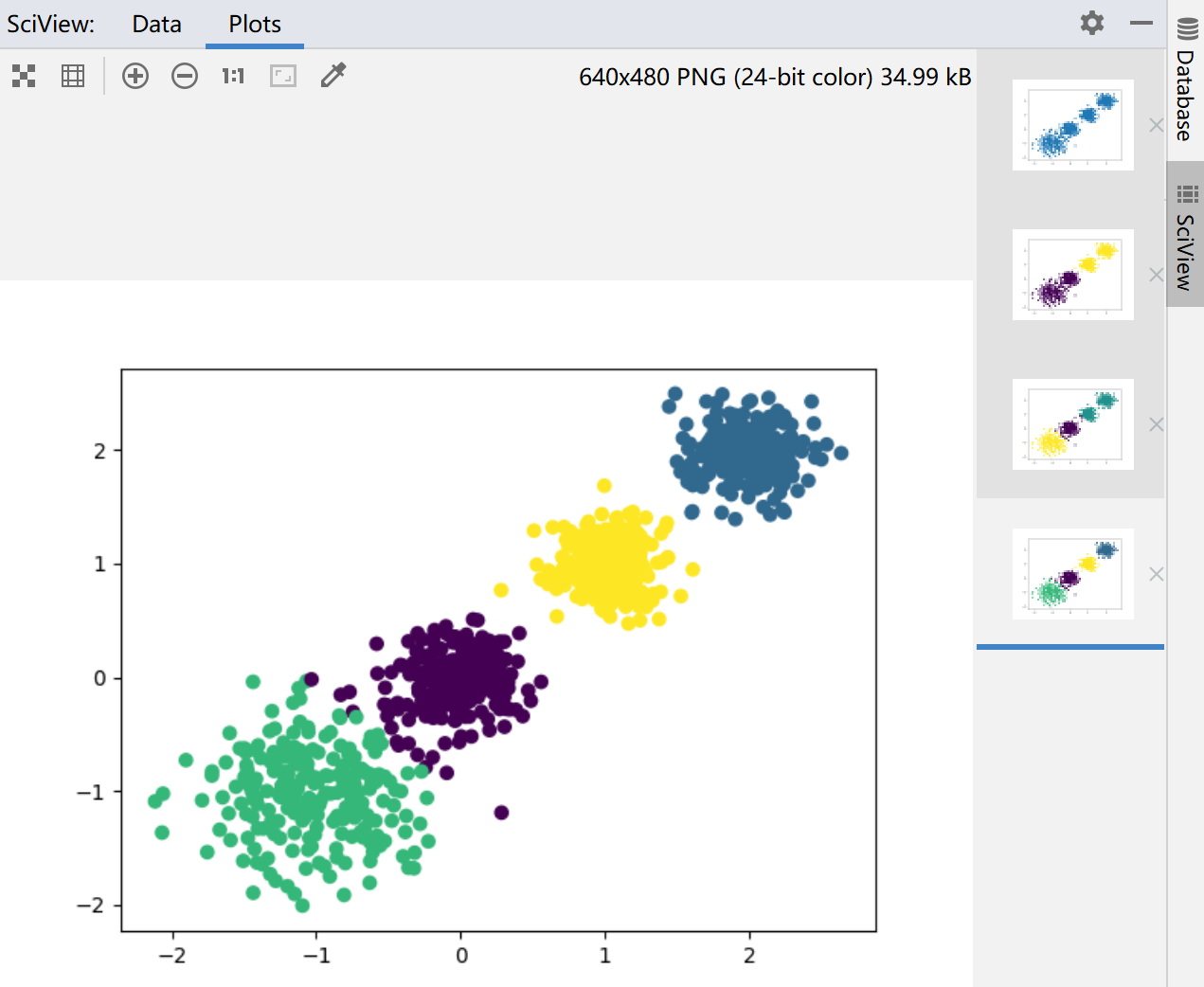
效果衡量

SSE：误差平方和

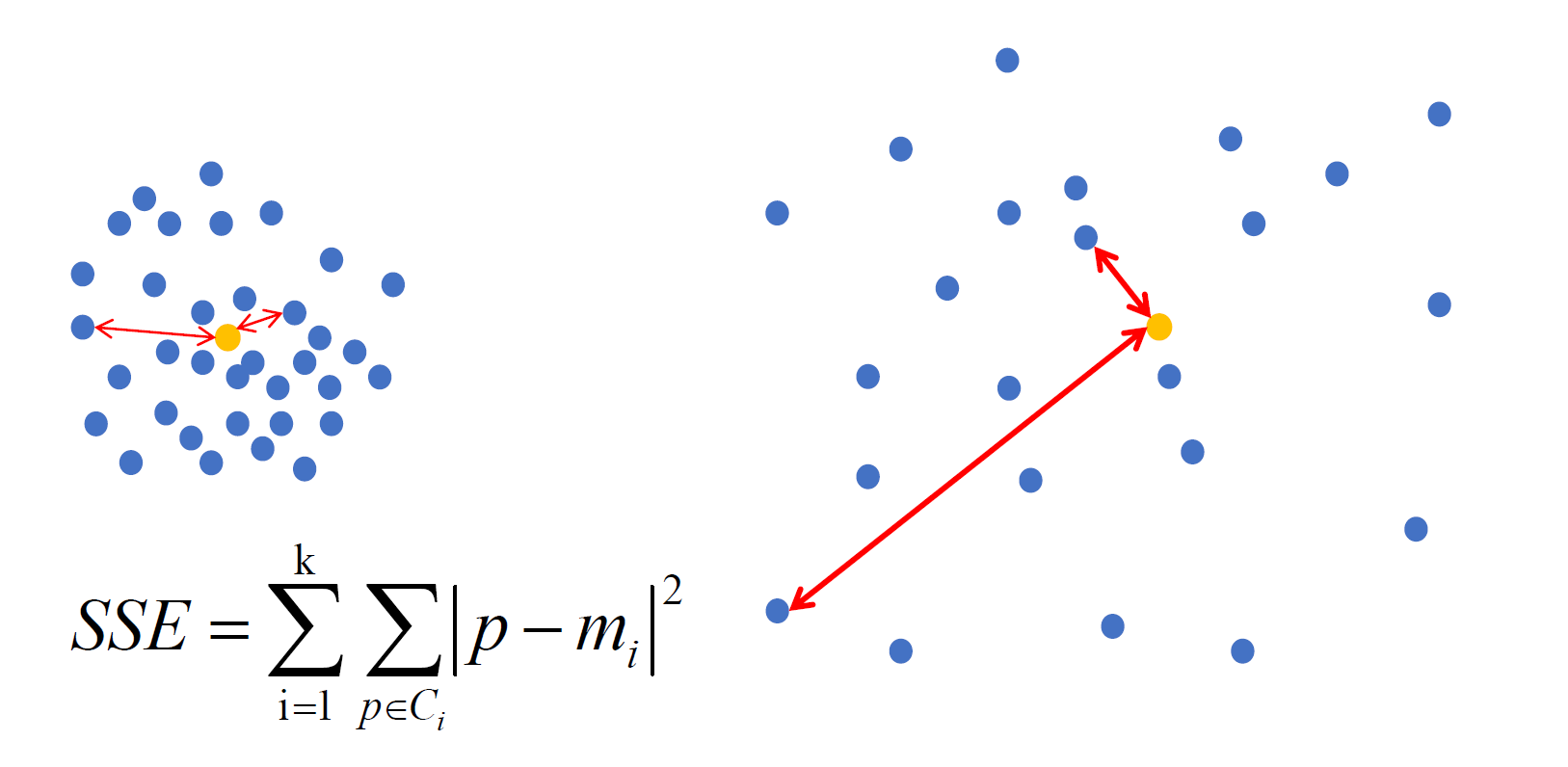
SSE(左图) < SSE(右图)

肘部法

Elbow method就是“肘”方法：

  1. 对于n个点的数据集，迭代计算k from 1 to n，每次聚类完成后计算每个点到其所属的簇中心的距离的平方和。
  2. 平方和是会逐渐变小的，直到k=n时平方和为0，因为每个点都是它所在的簇中心本身。
  3. 在这个平方和变化过程中，会出现一个拐点也即“肘”点，下降率突然变缓时即认为是最佳的K值。
import numpy as np
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt

# 生成数据
cluster1 = np.random.uniform(0.5, 1.5, (2, 10))
cluster2 = np.random.uniform(3.5, 4.5, (2, 10))
X = np.hstack((cluster1, cluster2)).T

# plt.figure()
# plt.axis([0, 5, 0, 5])
# plt.grid(True)
# plt.plot(X[:,0],X[:,1],'k.');

K = range(1, 10)
meandistortions = []
for k in K:
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    meandistortions.append(sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0])

plt.plot(K, meandistortions, 'bx-')
plt.xlabel('k')
# plt.ylabel('平均畸变程度',fontproperties=font)
plt.ylabel('Ave Distor')
# plt.title('用肘部法则来确定最佳的K值',fontproperties=font);
plt.title('Elbow method value K');
plt.show()

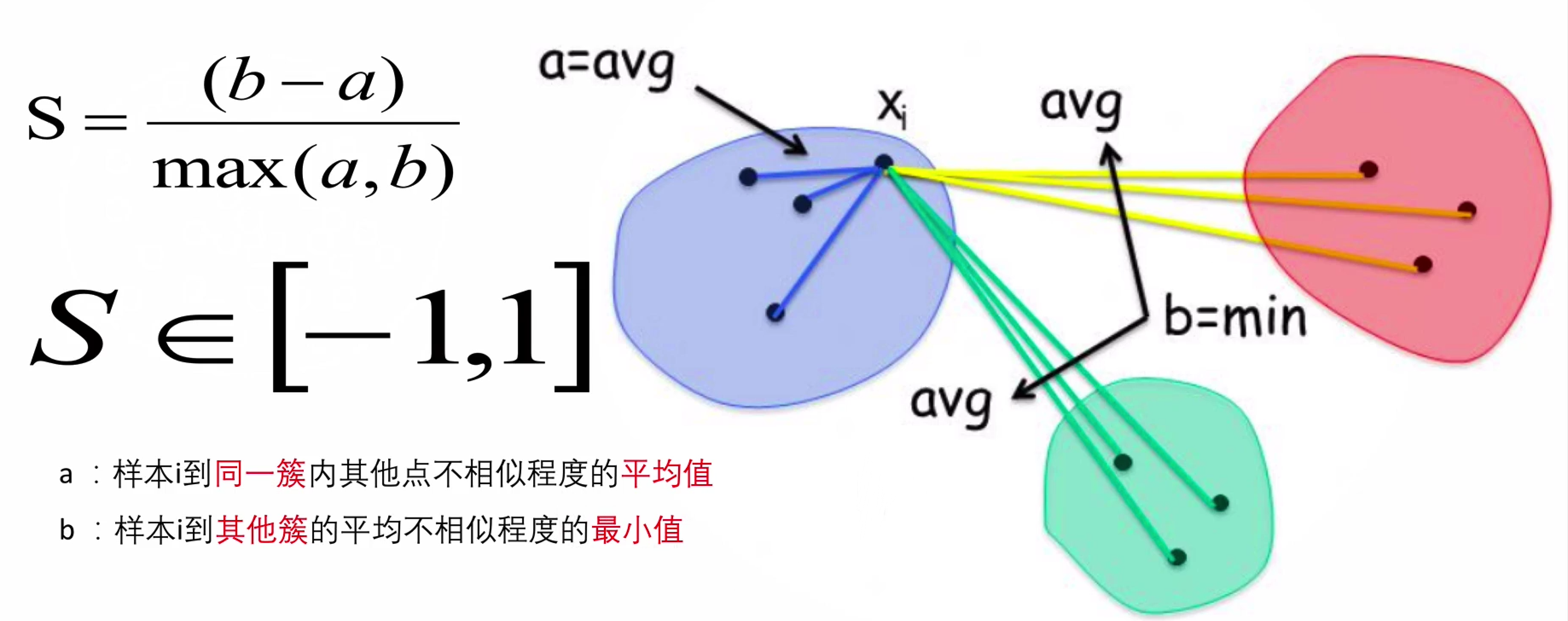
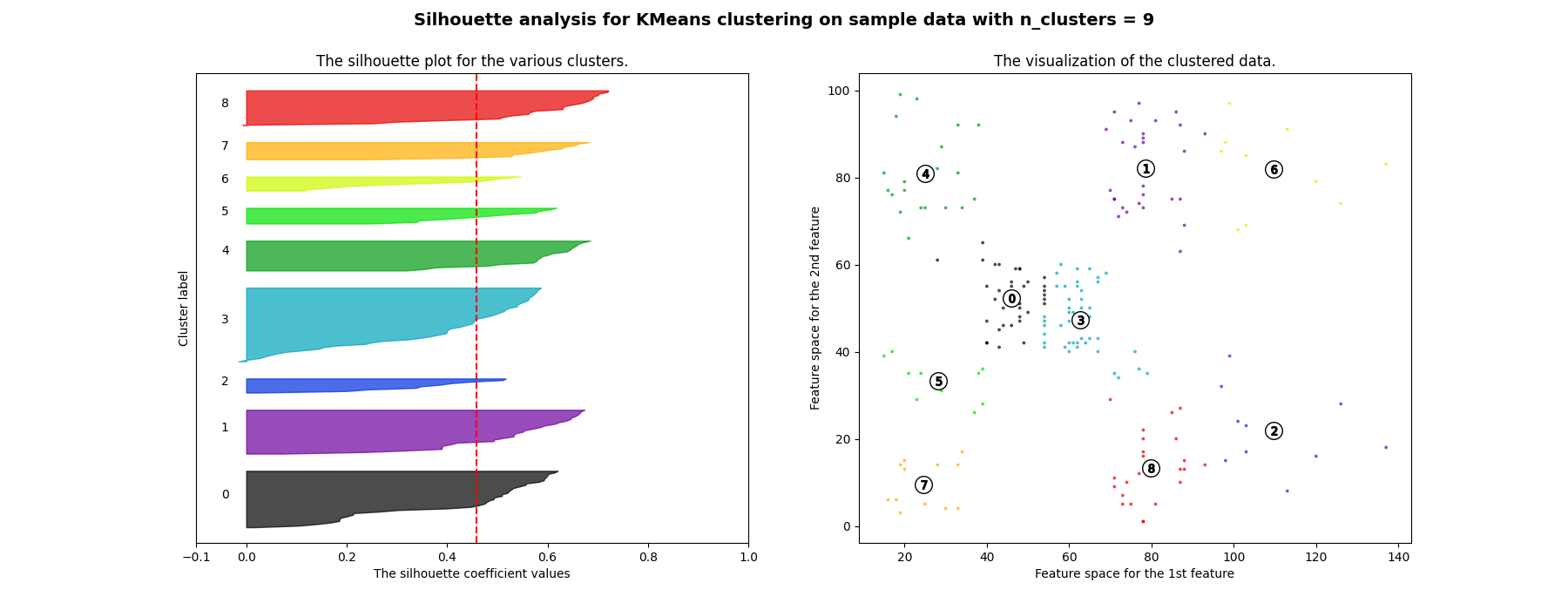
SC系数：轮廓系数法

结合了聚类的凝聚度（Cohesion）和分离度（Separation），用于评估聚类的效果。
（Silhouette Coefficient）

import numpy as np
import pandas as pd

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score

import matplotlib.pyplot as plt
import matplotlib.cm as cm
import seaborn as sns

input_data = pd.read_csv("./mall_customers.csv")

input_data.head()

input_data.shape

input_data.isnull().sum()

# selecting features
x = input_data.iloc[:,[3,4]].values

# Elbow Method

score = []

for cluster in range(1,11):
    kmeans = KMeans(n_clusters = cluster, init="k-means++", random_state=10)
    kmeans.fit(x)
    score.append(kmeans.inertia_)

# plotting the score

plt.plot(range(1,11), score)
plt.title('The Elbow Method')
plt.xlabel('no of clusters')
plt.ylabel('wcss')
plt.show()

# Silhouette score

for n_clusters in range(2,11):
    # Create a subplot with 1 row and 2 columns
    fig, (ax1, ax2) = plt.subplots(1, 2)
    fig.set_size_inches(18, 7)

    # The 1st subplot is the silhouette plot
    # The silhouette coefficient can range from -1, 1 but in this example all
    # lie within [-0.1, 1]
    ax1.set_xlim([-0.1, 1])
    # The (n_clusters+1)*10 is for inserting blank space between silhouette
    # plots of individual clusters, to demarcate them clearly.
    ax1.set_ylim([0, len(x) + (n_clusters + 1) * 10])

    # Initialize the clusterer with n_clusters value and a random generator
    # seed of 10 for reproducibility.
    clusterer = KMeans(n_clusters=n_clusters, random_state=10)
    cluster_labels = clusterer.fit_predict(x)

    # The silhouette_score gives the average value for all the samples.
    # This gives a perspective into the density and separation of the formed
    # clusters
    silhouette_avg = silhouette_score(x, cluster_labels)
    print("For n_clusters =", n_clusters,
          "The average silhouette_score is :", silhouette_avg)

    # Compute the silhouette scores for each sample
    sample_silhouette_values = silhouette_samples(x, cluster_labels)

    y_lower = 10
    for i in range(n_clusters):
        # Aggregate the silhouette scores for samples belonging to
        # cluster i, and sort them
        ith_cluster_silhouette_values = \
            sample_silhouette_values[cluster_labels == i]

        ith_cluster_silhouette_values.sort()

        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i

        color = cm.nipy_spectral(float(i) / n_clusters)
        ax1.fill_betweenx(np.arange(y_lower, y_upper),
                          0, ith_cluster_silhouette_values,
                          facecolor=color, edgecolor=color, alpha=0.7)

        # Label the silhouette plots with their cluster numbers at the middle
        ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

        # Compute the new y_lower for next plot
        y_lower = y_upper + 10  # 10 for the 0 samples

    ax1.set_title("The silhouette plot for the various clusters.")
    ax1.set_xlabel("The silhouette coefficient values")
    ax1.set_ylabel("Cluster label")

    # The vertical line for average silhouette score of all the values
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

    ax1.set_yticks([])  # Clear the yaxis labels / ticks
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

    # 2nd Plot showing the actual clusters formed
    colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
    ax2.scatter(x[:, 0], x[:, 1], marker='.', s=30, lw=0, alpha=0.7,
                c=colors, edgecolor='k')

    # Labeling the clusters
    centers = clusterer.cluster_centers_
    # Draw white circles at cluster centers
    ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
                c="white", alpha=1, s=200, edgecolor='k')

    for i, c in enumerate(centers):
        ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
                    s=50, edgecolor='k')

    ax2.set_title("The visualization of the clustered data.")
    ax2.set_xlabel("Feature space for the 1st feature")
    ax2.set_ylabel("Feature space for the 2nd feature")

    plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
                  "with n_clusters = %d" % n_clusters),
                 fontsize=14, fontweight='bold')

plt.show()

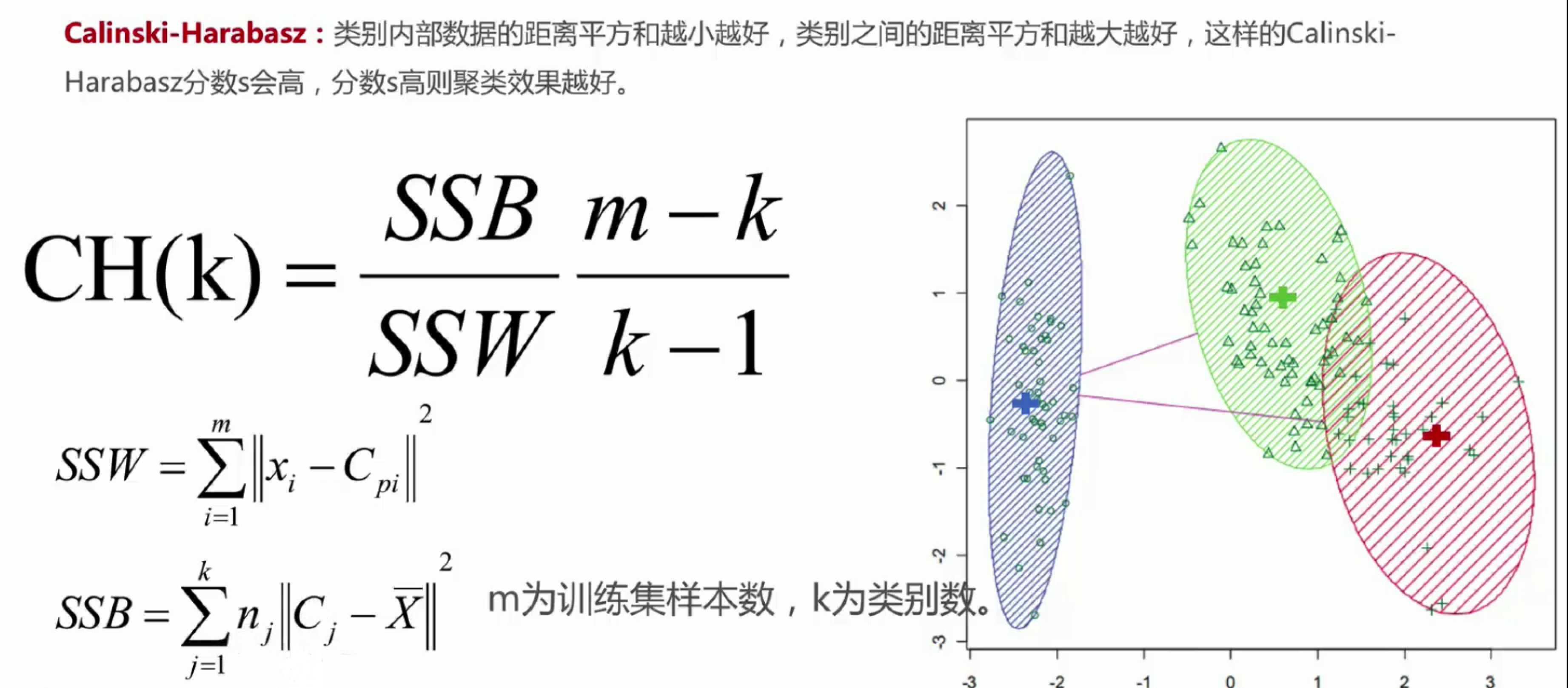
CH系数

算法优化

原始算法优缺点

优点

  1. 原理简单，容易实现。
  2. 聚类效果中上（依赖K的选择）。
  3. 空间复杂度$O(n)$，时间复杂度$O(I*K*N)$。（N为样本点数，K为中心点个数，I为迭代次数）

缺点

  1. 对离群点，噪声敏感（中心点易偏移）。
  2. 很难发现大小差别很大的簇及进行增量计算。
  3. 结果不一定是全局最优，只能保证局部最优（与K的个数及初值选取有关）。

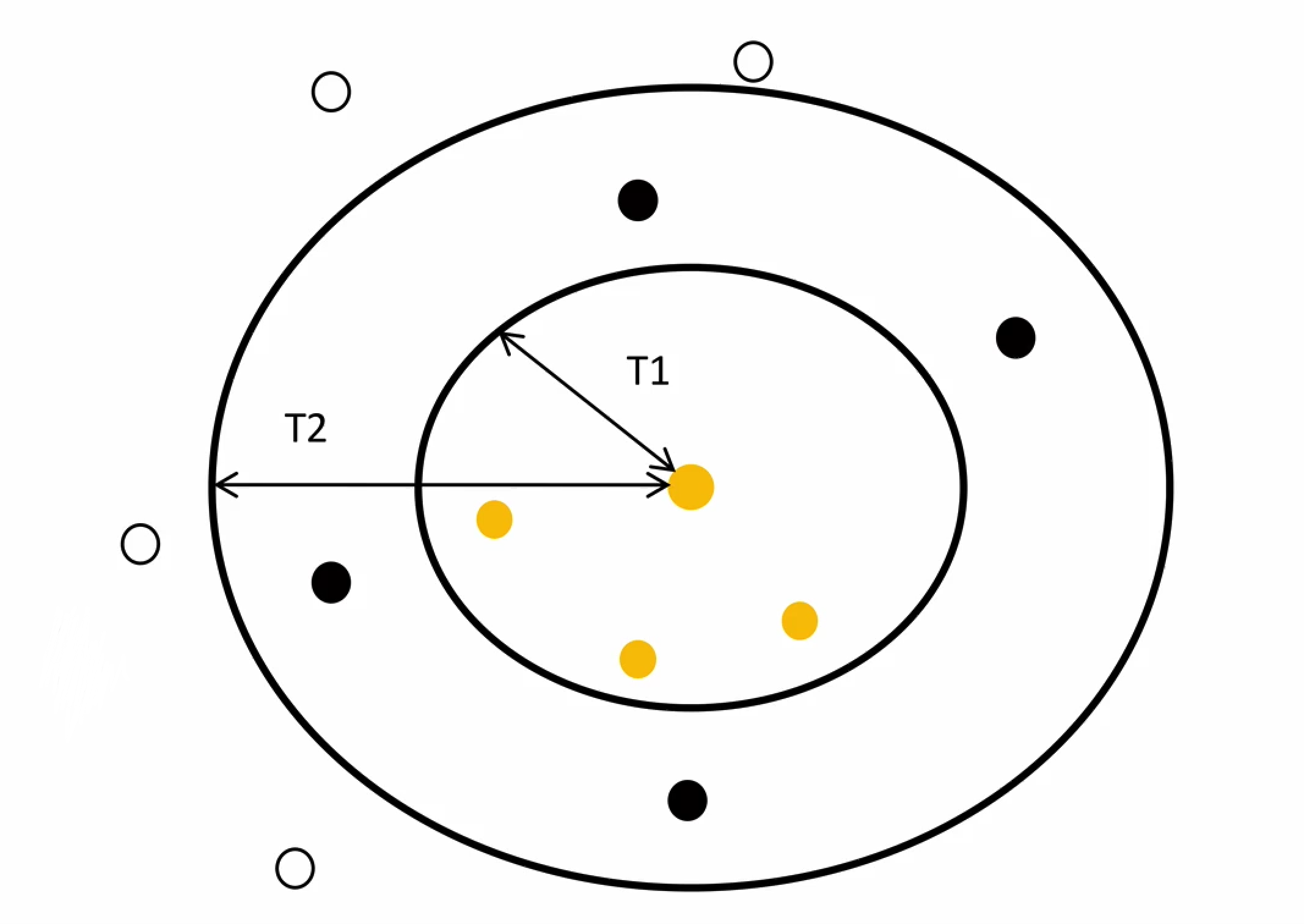
Canopy算法配合初始聚类

Canopy算法的作用在于它是通过事先粗聚类的方式，为K-means算法确定初始聚类中心个数和聚类中心点。

优点：

  1. K-means对噪声抗干扰较弱，通过Canopy对比，将较小的NumPoint的Cluster直接去掉有利于抗干扰。
  2. Canopy选择出来的每个Canopy的centerPoint作为K会更精确。
  3. 只是针对每个Canopy的内做K-means聚类，减少相似计算的数量。

不足：

  1. 算法中T1, T2的确定问题。

K-means++

$P=\frac{D(x)^2}{ {\textstyle \sum_{x\in X}^{}D(x)^2} }$

K-Means++算法采用下列步骤给定K个初始质点：

  1. 从数据集中任选一个节点作为第一个聚类中心。
  2. 对数据集中的每个点x，计算x到所有已有聚类中心点的距离和D(X)，基于D(X)采用线性概率选择出下一个聚类中心点(距离较远的一个点成为新增的一个聚类中心点)。
  3. 重复步骤2直到找到K个聚类中心点。

缺点：由于聚类中心点选择过程中的内在有序性，在扩展方面存在着性能方面的问题(第K个聚类中心点的选择依赖前K-1个聚类中心点的值)

二分K-means

解决K-Means算法对初始簇心比较敏感的问题，二分K-Means算法是一种弱化初始质心的一种算法，具体思路步骤如下：

1、将所有样本数据作为一个簇放到一个队列中。
2、从队列中选择一个簇进行K-means算法划分，划分为两个子簇，并将子簇添加到队列中。
3、循环迭代第二步操作，直到中止条件达到(聚簇数量、最小平方误差、迭代次数等)。
4、队列中的簇就是最终的分类簇集合。

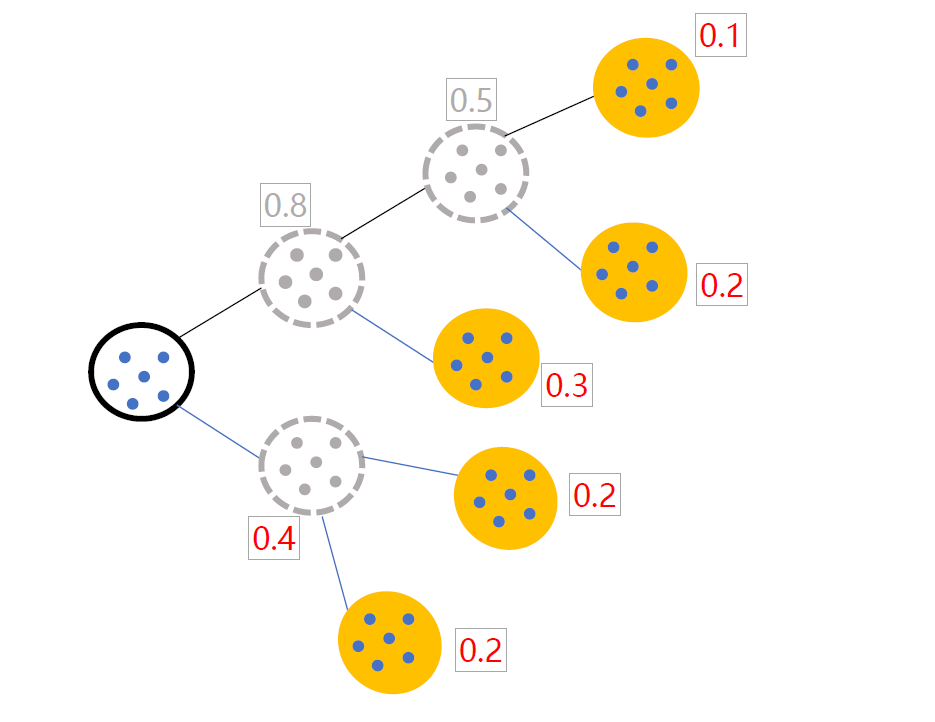
Kernel K-means

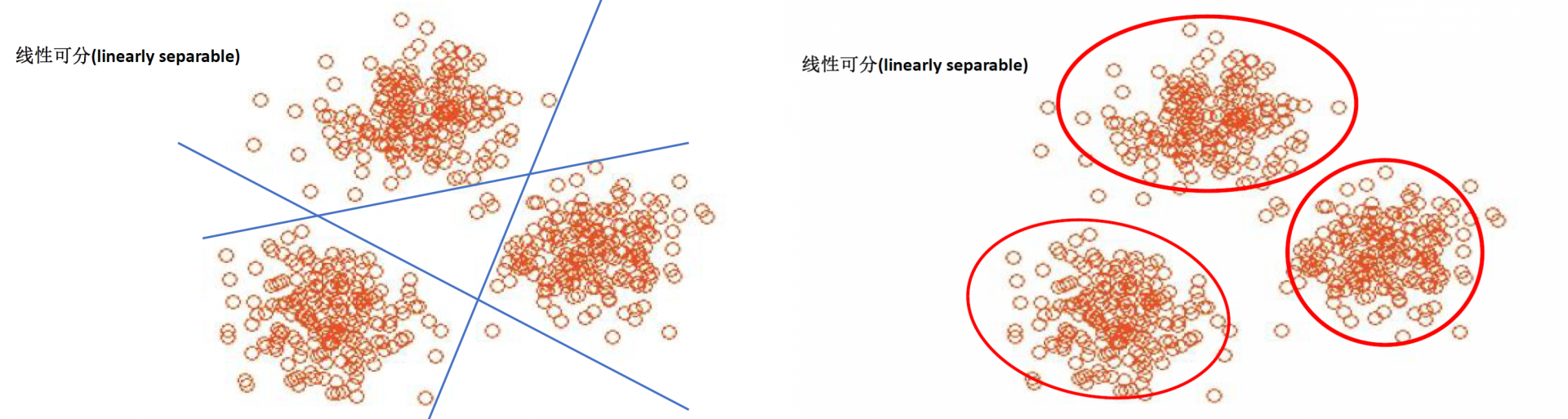
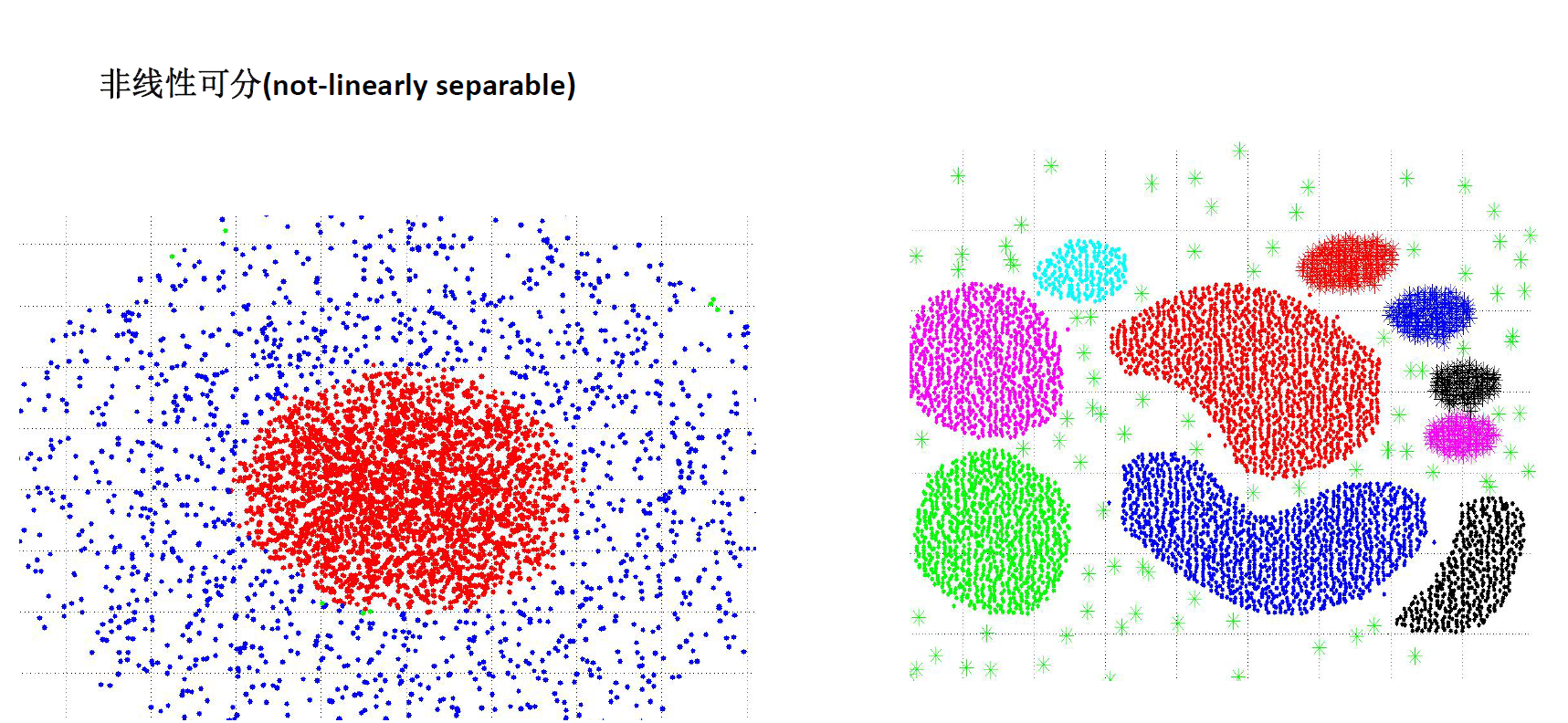
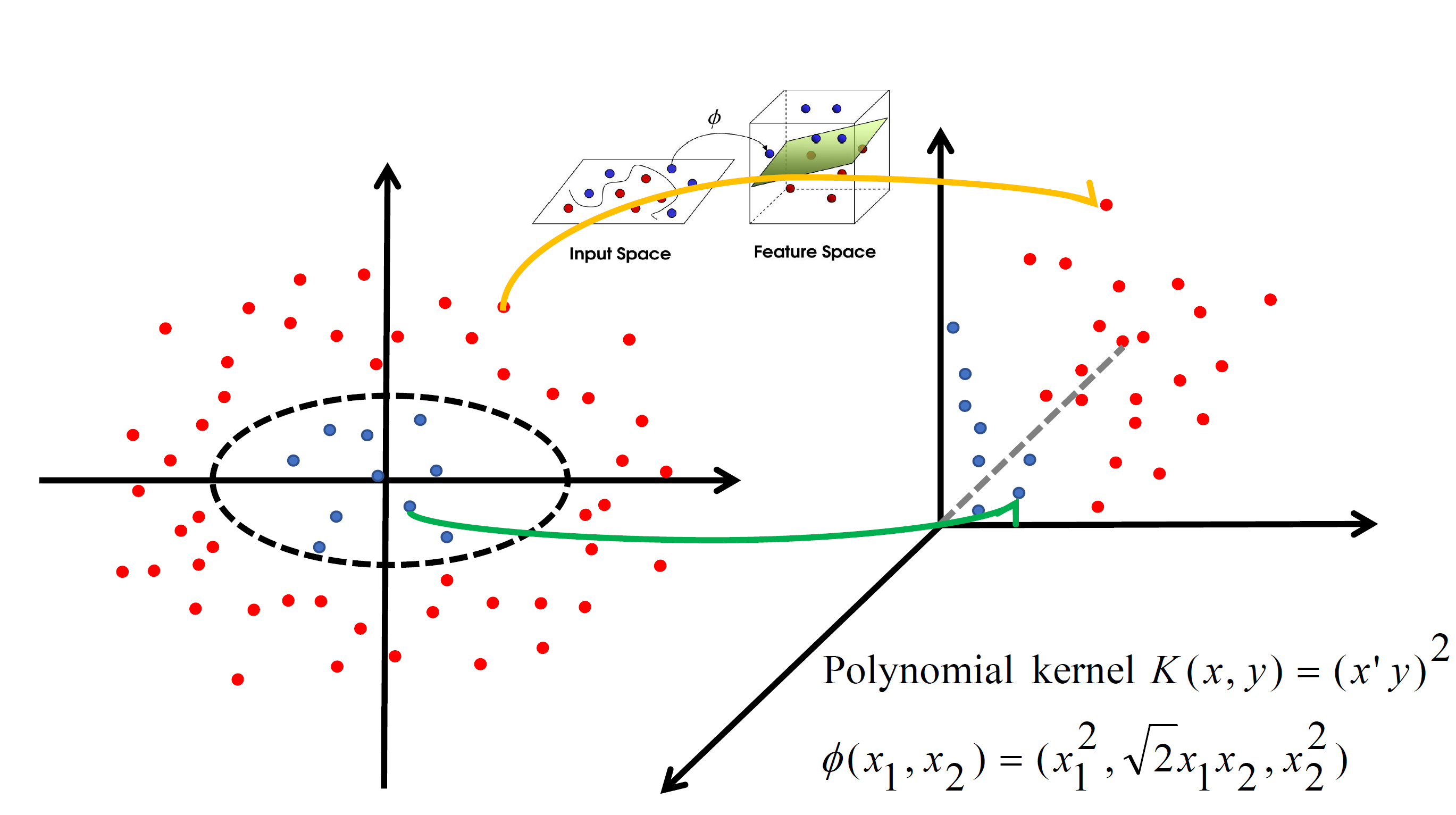
Kernel K-means，将每个样本进行一个投射到高维空间的处理，然后再将处理后的数据使用普通的k-means算法思想进行聚类。

K-medoids

K-medoids和K-means是有区别的，不一样的地方在于中心点的选取：

  • K-means中，将中心点取为当前cluster中所有数据点的平均值，对异常点很敏感。
  • K-medoids中，将从当前cluster 中选取到其他所有（当前cluster中的）点的距离之和最小的点作为中心点。

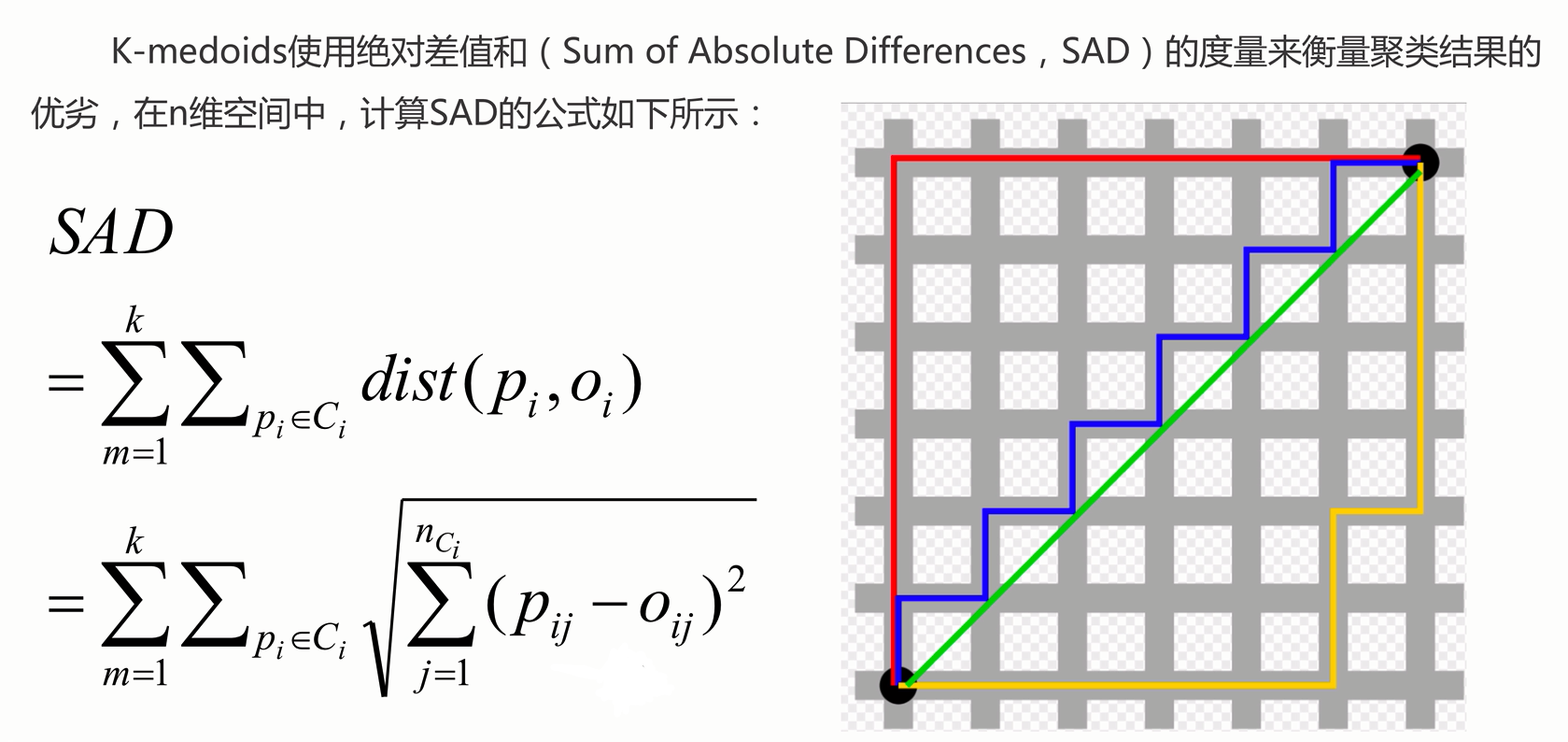
算法流程：

  1. 总体n个样本点中任意选取k个点作为medoids。
  2. 按照与medoids最近的原则，将剩余的n-k个点分配到当前最佳的medoids代表的类中。
  3. 对于第i个类中除对应medoids点外的所有其他点，按顺序计算当其为新的medoids时，代价函数的值，遍历所有可能，选取代价函数最小时对应的点作为新的medoids。
  4. 重复2-3的过程，直到所有的medoids点不再发生变化或已达到设定的最大迭代次数。
  5. 产出最终确定的k个类。

优缺点：

  • K-medoids对噪声的鲁棒性好。
  • K-medoids只能对小样本起作用，样本大速度太慢。
  • K-medoids较K-means来说，多次运行每次结果偏差较小，而k-means对初值依赖大，导致每次运行结果相异程度大。

对比：

ISODATA

Interative Self Organizing Data Anslysis Techniques Algorithm

K-means和K-means++的聚类中心数K是固定不变的。而ISODATA算法在运行过程中能够根据各个类别的实际情况进行两种操作来调整聚类中心数K：(1)分裂操作，对应着增加聚类中心数；(2)合并操作，对应着减少聚类中心数。

该算法能够在聚类过程中根据各个类所包含样本的实际情况动态调整聚类中心的数目。如果某个类中样本分散程度较大（通过方差进行衡量）并且样本数量较大，则对其进行分裂操作；如果某两个类别靠得比较近（通过聚类中心的距离衡量），则对它们进行合并操作。

Mini Batch K-Means

适合大数据的聚类算法。

Mini Batch KMeans使用了Mini Batch（分批处理）的方法对数据点之间的距离进行计算。
Mini Batch计算过程中不必使用所有的数据样本，而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本量少，所以会相应的减少运行时间，但另一方面抽样也必然会带来准确度的下降。

步骤：

  1. 从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心。
  2. 更新质心。

区别：
与K-means相比，数据的更新在每一个小的样本集上。对于每一个小批量，通过计算平均值得到更新质心，并把小批量里的数据分配给该质心，随着迭代次数的增加，这些质心的变化是逐渐减小的，直到质心稳定或者达到指定的迭代次数，停止计算。

算法进阶

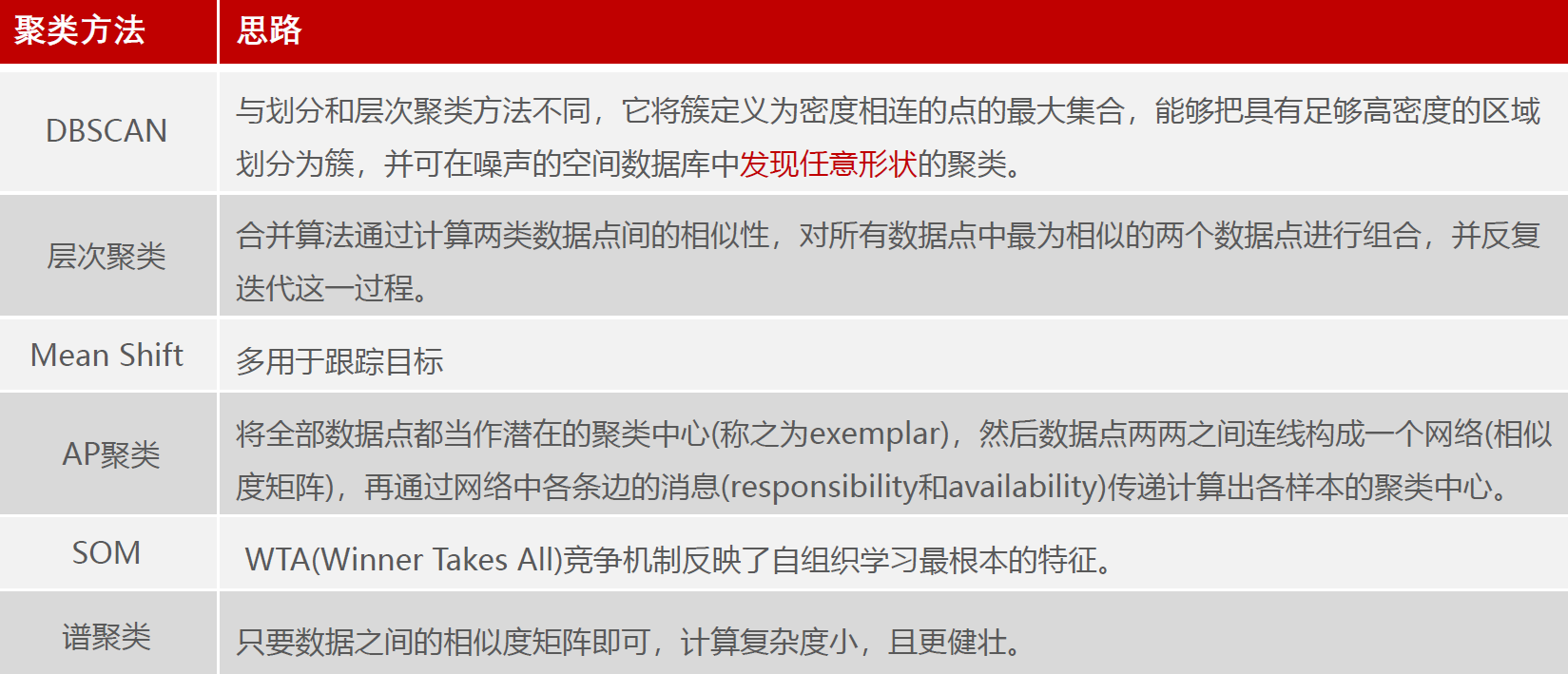
DBSCAN(基于密度聚类)

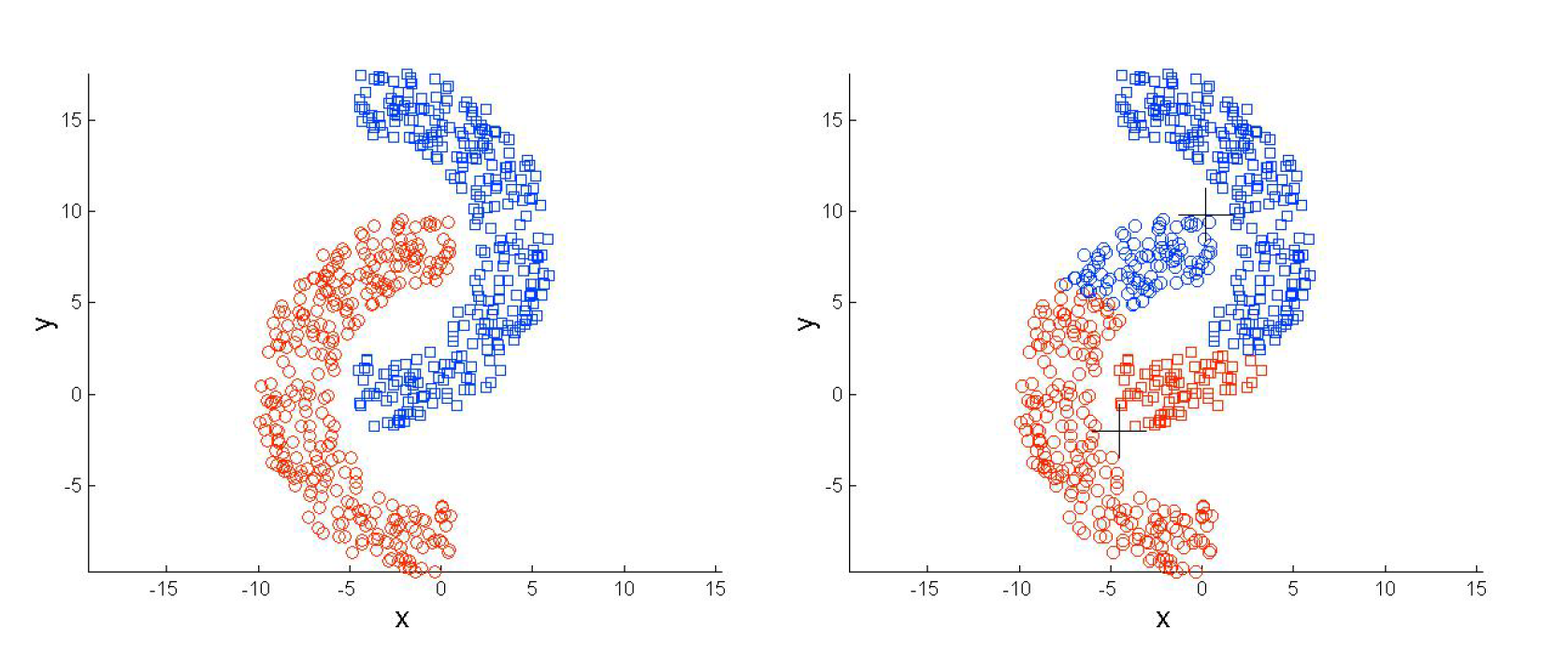
  • 参数1：半径（Eps），表示以给定点P为中心的圆形邻域的范围。
  • 参数2：以点P为中心的邻域内最少点的数量（MinPts）。

如果满足：以点P为中心、半径为Eps的邻域内的点的个数不少于MinPts，则称点P为核心点。

步骤：

  1. 将所有点标记为核心点，边界点或噪声点。
  2. 删除噪声点。
  3. 为距离在Eps之内的所有核心点之间赋予一条边。
  4. 每组连通的核心点形成一个簇。
  5. 讲每个边界点都指派到一个与之关联的核心点的簇中。

优点：

  1. 聚类速度快且能够有效处理噪声点和发现任意形状的空间聚类。
  2. 与K-Means比较，不需要输入要划分的聚类个数。
  3. 可以在需要输入过滤噪声的参数，且聚类簇形状较稳定可靠。

缺点：

  1. 数据量增大时，要求较大的内存支持且I/O消耗也很大。
  2. 当聚类的密度不均匀、聚类间距相差很大时，聚类质量较差，此时参数MinPts和Eps选取困难。
  3. 算法聚类效果依赖于距离公式选取，实际应用中常用欧氏距离，对于高维数据，存在“维数灾难”。

OPTICS(Ordering points to identify the clustering structure)是一基于密度的聚类算法，OPTICS算法是DBSCAN的改进版本。

层次聚类

先计算样本之间的距离。每次将距离最近的点合并到同一个类。然后，再计算类与类之间的距离，将距离最近的类合并为一个大类。不停的合并，直到合成了一个类。其中类与类的距离的计算方法有：最短距离法，最长距离法，中间距离法，类平均法等。

  • MIN度量
  • MAX度量
  • Group Average（平均距离度量）
  • Distance Between Centroids（质心度量）
  • Other methods driven by an objective function

层次聚类可以分为两种主要类型：凝聚型（agglomerative）和分裂型（divisive）。

  1. 凝聚聚类：它也被称为AGNES（凝聚嵌套）。 它以自下而上的方式工作。 也就是说，每个对象最初被认为是单元素簇（叶子）。 在算法的每个步骤中，将最相似的两个群集组合成新的更大的群集（节点）。 迭代此过程，直到所有点都只是一个单个大簇（root）的成员（参见下图）。 结果是一棵树，可以绘制为树状图。
  2. 分裂层次聚类：它也被称为DIANA（Divise Analysis），它以自上而下的方式工作。 该算法是AGNES的逆序。 它以root开头，其中所有对象都包含在单个集群中。 在迭代的每个步骤中，最异构的集群被分成两个。 迭代该过程，直到所有对象都在它们自己的集群中（见下图）。

其中，凝聚聚类擅长识别小聚类。 分裂层次聚类擅长识别大型集群。

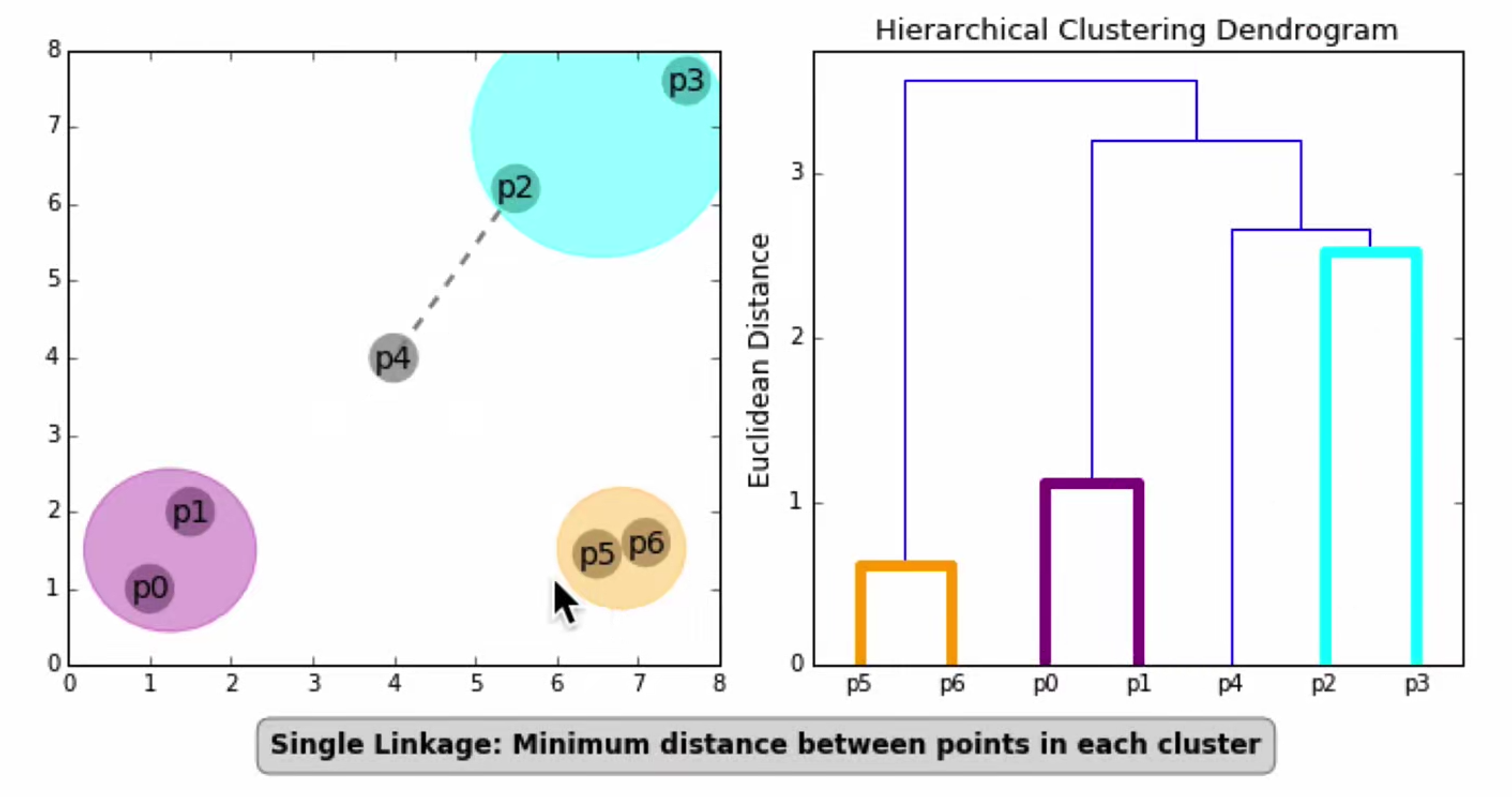
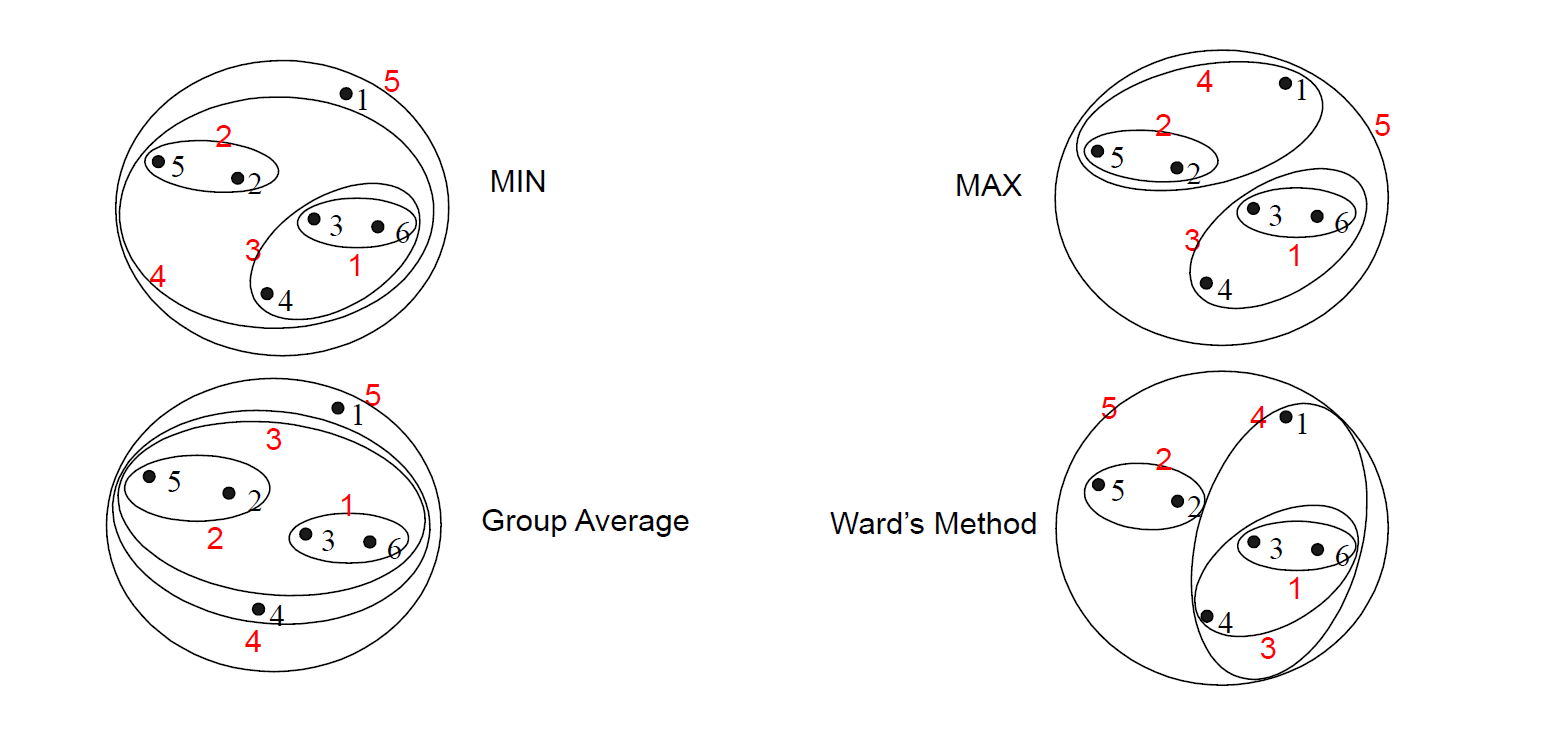
步骤：

  1. 孤点：将每个对象看作一类，计算两两之间的最小距离。
  2. 合并：将距离最小的两类合并成一个新类。
  3. 迭代：重新计算新类与所有类之间的距离。
  4. 统一：重复(2)(3)直到所有类最后合并成一类。

优点：

  1. 距离相似度易定义，限制少。
  2. 不需要预先制定聚类数。
  3. 可以发现类的层次关系。

缺点：

  1. 合并决策是最终的。一旦合并，不可撤销。
  2. 计算复杂度较高。
  3. 奇异值易产生很大影响，算法很可能聚类成链状。

应用：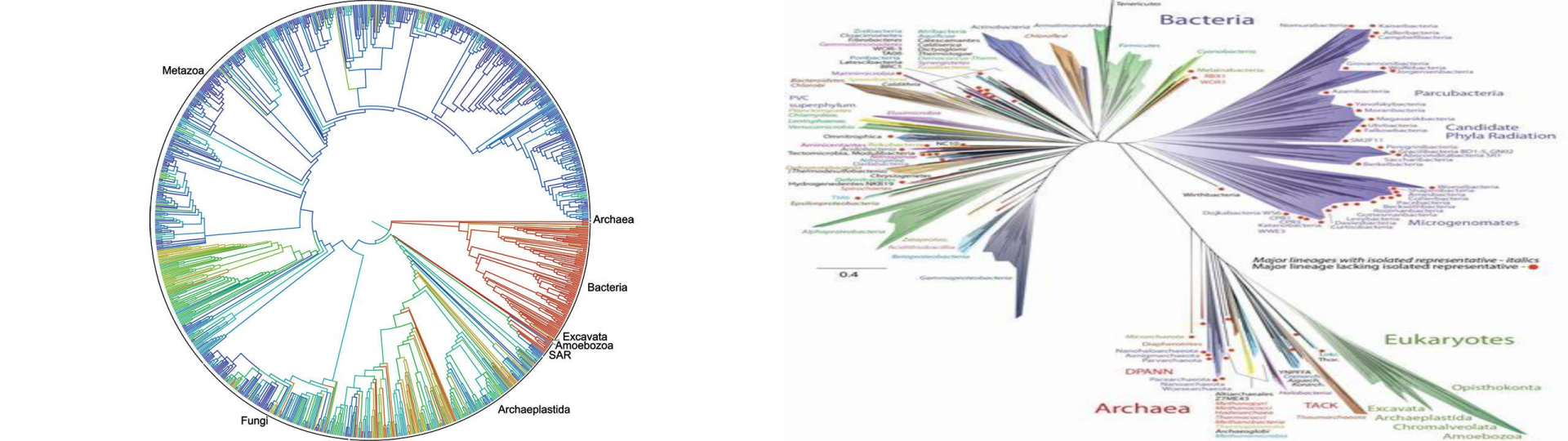

Mean Shift聚类

Mean Shift（均值漂移）是基于密度的非参数聚类算法，其算法思想是假设不同簇类的数据集符合不同的概率密度分布，找到任一样本点密度增大的最快方向（最快方向的含义就是Mean Shift），样本密度高的区域对应于该分布的最大值，这些样本点最终会在局部密度最大值收敛，且收敛到相同局部最大值的点被认为是同一簇类的成员。

Affinity Propagation (AP)聚类

AP(Affinity Propagation)算法,称为仿射传播聚类算法、近邻传播聚类算法、亲和传播聚类算法，是根据数据点之间的相似度来进行聚类，可以是对称的，也可以是不对称的。该算法不需要先确定聚类的数目，而是把所有的数据点都看成潜在意义上的聚类中心（exemplar）。

优点：

  1. 不需要制定最终聚类族的个数。
  2. 已有的数据点作为最终。的聚类中心， 而不是新生成一个族中心。
  3. 模型对数据的初始值不敏感。
  4. 对初始相似度矩阵数据的对称性没有要求。

缺点：

  1. AP算法需要事先计算每对数据对象之间的相似度， 如果数据对象太多的话， 内存放不下，若存在数据库， 频繁访问数据库也需要时间。
  2. AP算法的时间复杂度较高，一次迭代大概$O(N^3)$
  3. 聚类的好坏受到参考度和阻尼系数的影响。

扩展：
Label Propagation 算法是一种基于标签传播的局部社区划分算法。对于网络中的每一个节点，在初始阶段，Label Propagation 算法对每个节点初始化一个唯一的标签，在每次的迭代过程中，每个节点根据与其相连的节点所属的标签改变自己的标签，更改的原则是选择与其相连的节点中所属标签最多的社区标签为自己的社区标签，这便是标签传播的含义。随着社区标签不断传播，最终，连接紧密的节点将有共同的标签。

Label Propagation算法包括两大步骤：(1)构造相似矩阵；(2)标签传播。

SOM聚类

SOM 即自组织映射，是一种用于特征检测的无监督学习神经网络。它模拟人脑中处于不同区域的神经细胞分工不同的特点，即不同区域具有不同的响应特征，而且这一过程是自动完成的。SOM 用于生成训练样本的低维空间，可以将高维数据间复杂的非线性统计关系转化为简单的几何关系，且以低维的方式展现，因此通常在降维问题中会使用它。

SOM 的训练过程：
紫色区域表示训练数据的分布状况，白色网格表示从该分布中提取的当前训练数据。

  1. SOM 节点位于数据空间的任意位置，最接近训练数据的节点（黄色高亮部分）会被选中。它和网格中的
    邻近节点一样，朝训练数据移动。
  2. 在多次迭代之后，网格倾向于近似该种数据分布（下图最右）

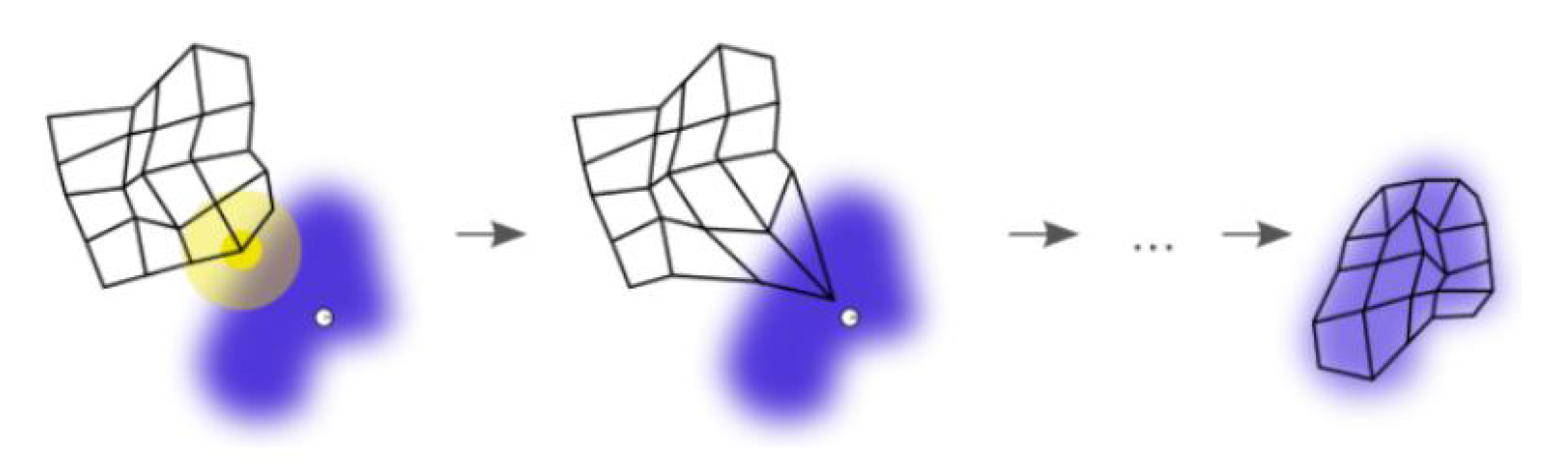
步骤：

  1. 将网格的神经元随机定位在数据空间中。
  2. 选择一个数据点，按顺序随机或系统地循环遍历数据集
  3. 找到最接近所选数据点的神经元。这种神经元被称为最佳匹配单元BMU。
  4. 将BMU移近该数据点。 BMU移动的距离由学习速率确定，学习速率在每次迭代后减小。
  5. 将BMU的邻居移动到更靠近该数据点的位置，远处的邻居移动得更少。使用BMU周围的半径
    来识别邻居，并且在每次迭代之后该半径的值减小。
  6. 在重复步骤1到4之前，更新学习速率和BMU半径。迭代这些步骤，直到神经元的位置稳定。

应用：
SOM 通常用在可视化中。比如右图，世界各国贫困数据的可视化。生活质量较高的国家聚集在左上方，而贫困最严重的国家聚集在右下方。

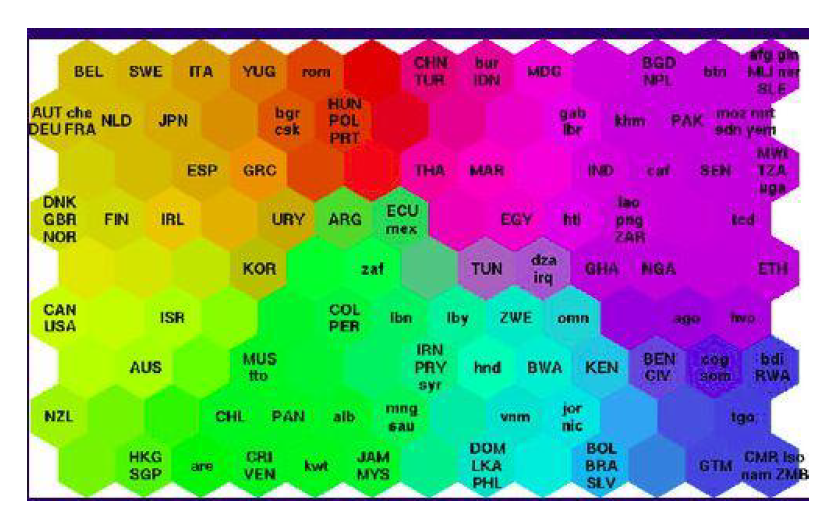
  • 数据压缩
  • 语音识别
  • 分离音源
  • 欺诈检测

谱聚类

谱聚类：是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类。

图（Graph）：由若干点及连接两点的线所构成的图形，通常用来描述某些事物之间的某种关系，用点代表事物，线表示对应两个事物间具有这种关系。

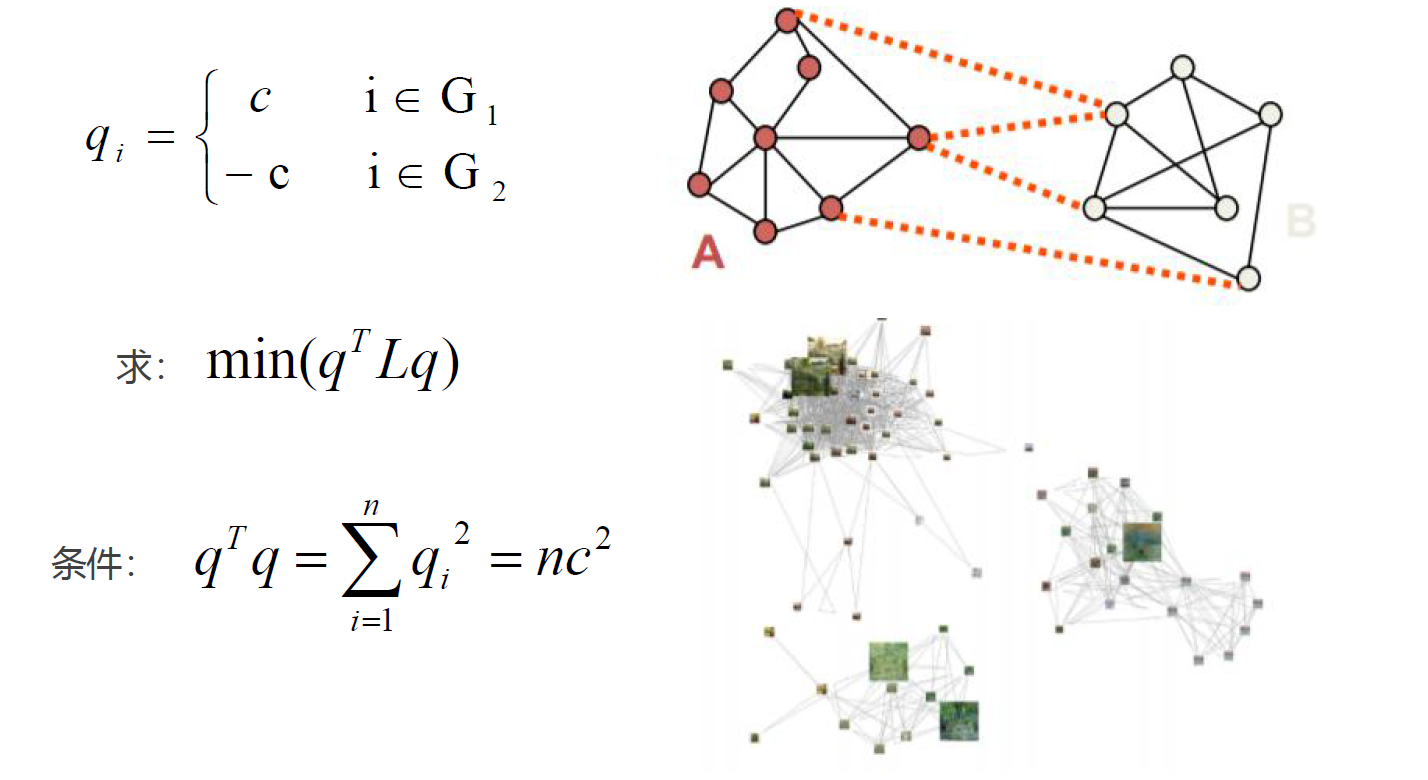
优点：

  1. 稀疏处理：谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效。
  2. 高维处理：使用了降维，因此在处理高维数据聚类时的复杂度比传统聚类算法好，在高维数据上的表现尤为明显。

缺点：

  1. K值只能靠猜测。
  2. 聚类效果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能不同。

总结

参考链接：

版权属于：moluuser

本文链接：https://archive.moluuser.com/archives/80/

知识共享许可协议
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。


正文到此结束


扫一扫在手机打开当前页
© 允许规范转载

【我要纠错】