要头发干嘛 
03. 数组中重复的数字
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3 限制:
2 <= n <= 100000代码:
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
pair<set<int>::iterator, bool> retpair;
set<int> set;
for(int num: nums) {
retpair = set.insert(num);
if(retpair.second == false)
return num;
}
return -1;
}
};class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
int i = 0;
while(i < nums.size()) {
if(nums[i] == i) {
++i;
continue;
}
if(nums[nums[i]] == nums[i])
return nums[i];
swap(nums[i], nums[nums[i]]);
}
return -1;
}
};04. 二维数组中的查找
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。限制:
0 <= n <= 1000
0 <= m <= 1000代码:
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int i = matrix.size() - 1;
int j = 0;
while(i >= 0 && j < matrix[0].size()) {
if (matrix[i][j] > target) i--;
else if (matrix[i][j] < target) j++;
else return true;
}
return false;
}
};05. 替换空格
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
示例 1:
输入:s = "We are happy."
输出:"We%20are%20happy."限制:
0 <= s 的长度 <= 10000代码:
class Solution {
public:
string replaceSpace(string s) {
int len = s.size();
int cnt = 0;
// 获取空格数
for(char c: s) {
if (c == ' ')
cnt++;
}
// 修改s长度
s.resize(len + 2 * cnt);
// 指向原字符串尾部
int i = len - 1;
// 指向新字符串尾部
int j = s.size() - 1;
for(; i < j; i--, j--) {
if(s[i] != ' ')
s[j] = s[i];
else {
s[j - 2] = '%';
s[j - 1] = '2';
s[j] = '0';
j -= 2;
}
}
return s;
}
};class Solution {
public:
string replaceSpace(string s) {
int pos = s.find(" ");
while (pos != -1) {
// 将字符串中以某个位置开始的指定长度替换为目前字符串
s = s.replace(pos, 1, "%20");
pos = s.find(" ");
}
return s;
}
};06. 从尾到头打印链表
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
示例 1:
输入:head = [1,3,2]
输出:[2,3,1]限制:
0 <= 链表长度 <= 10000代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
ListNode* p = head;
vector<int> arr;
while (NULL != p) {
arr.push_back(p->val);
p = p->next;
}
reverse(arr.begin(), arr.end());
return arr;
}
};07. 重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]返回如下的二叉树:
3
/ \
9 20
/ \
15 7限制:
0 <= 节点个数 <= 5000代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
int index = 0;
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
TreeNode* head = nullptr;
int left = 0;
int right = inorder.size();
head = reBuild(preorder, inorder, left, right);
return head;
}
TreeNode* reBuild(vector<int>& preorder, vector<int>& inorder, int left, int right) {
if(index == preorder.size() || left == right)
return nullptr;
TreeNode* head = nullptr;
for(int i = left; i < right; i++) {
// 寻找根节点
if(preorder[index] == inorder[i]) {
head = new TreeNode(preorder[index]);
// 前序遍历中index后移
index++;
head->left = reBuild(preorder, inorder, left, i);
head->right = reBuild(preorder, inorder, i + 1, right);
break;
}
}
return head;
}
};09. 用两个栈实现队列
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
示例 1:
输入:
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出:[null,null,3,-1]
示例 2:输入:
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]
输出:[null,-1,null,null,5,2]提示:
1 <= values <= 10000
最多会对 appendTail、deleteHead 进行 10000 次调用代码:
class CQueue {
stack<int> stack1, stack2;
public:
CQueue() {
}
void appendTail(int value) {
stack1.push(value);
}
int deleteHead() {
if(stack2.empty()) {
while(!stack1.empty()) {
stack2.push(stack1.top());
stack1.pop();
}
}
if(stack2.empty()) {
return -1;
}else {
int delVal = stack2.top();
stack2.pop();
return delVal;
}
}
};
/**
* Your CQueue object will be instantiated and called as such:
* CQueue* obj = new CQueue();
* obj->appendTail(value);
* int param_2 = obj->deleteHead();
*/10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1示例 2:
输入:n = 5
输出:5提示:
0 <= n <= 100代码:
class Solution {
public:
int fib(int n) {
int a = 0, b = 1, sum = 0;
for(int i = 0; i < n; i++) {
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return a;
}
};思路:
循环求余法:
大数越界: 随着 $n$ 增大, $f(n)$ 会超过 Int32 甚至 Int64 的取值范围,导致最终的返回值错误。
- 求余运算规则: 设正整数 $x, y, p$ 求余符号为 $\odot$ ,则有 $(x + y) \odot p = (x \odot p + y \odot p) \odot p$ 。
- 解析: 根据以上规则,可推出 $f(n) \odot p = [f(n-1) \odot p + f(n-2) \odot p] \odot p$ ,从而可以在循环过程中每次计算 $sum = (a + b) \odot 1000000007$ ,此操作与最终返回前取余等价。

10- II. 青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2示例 2:
输入:n = 7
输出:21示例 3:
输入:n = 0
输出:1提示:
0 <= n <= 100代码:
class Solution {
public:
int numWays(int n) {
n = n + 1;
int a = 0, b = 1, sum = 0;
for(int i = 0; i < n; i++) {
sum = (a + b) % 1000000007;
a = b;
b = sum;
}
return a;
}
};11. 旋转数组的最小数字
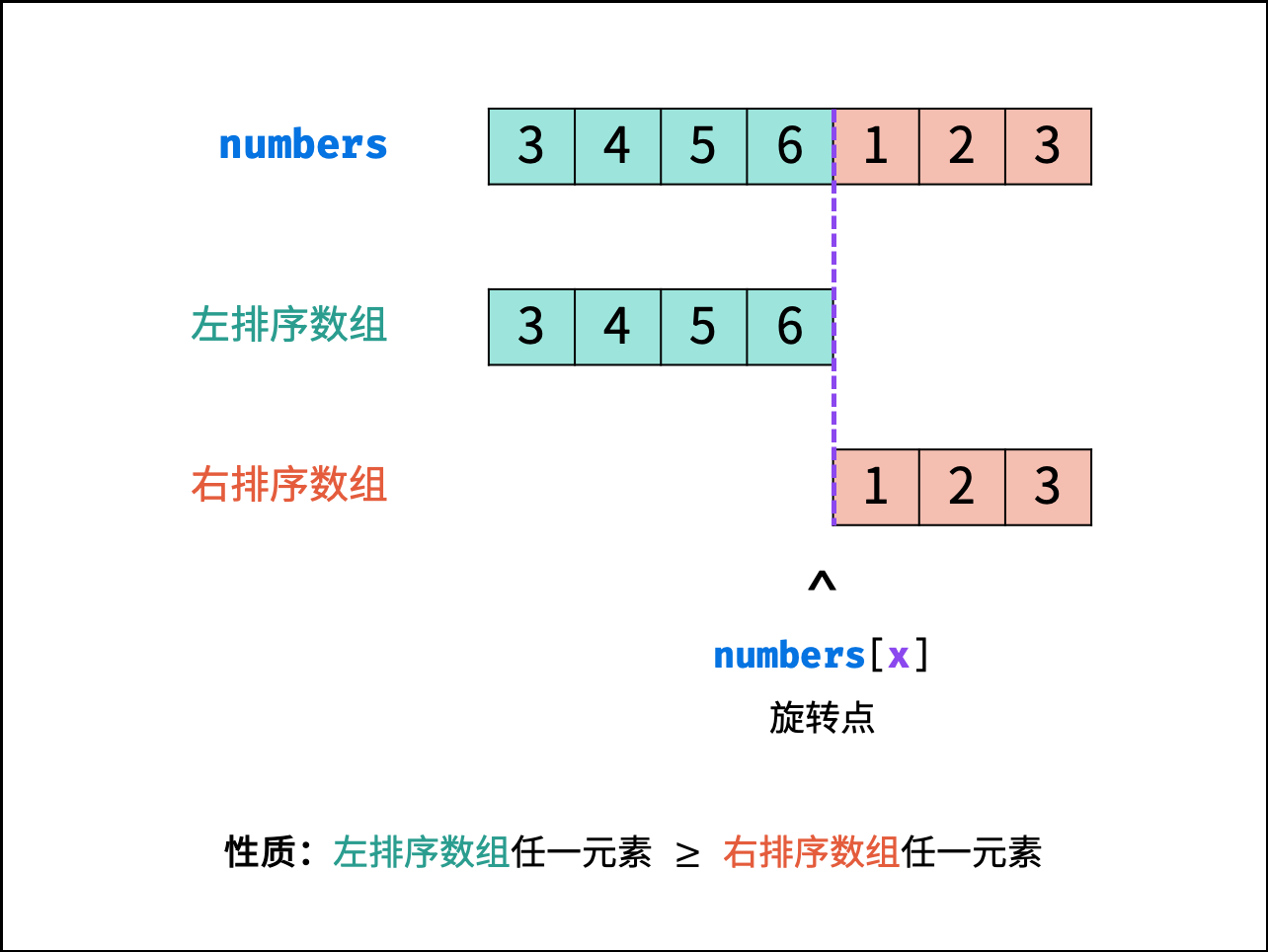
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
示例 1:
输入:[3,4,5,1,2]
输出:1示例 2:
输入:[2,2,2,0,1]
输出:0代码:
class Solution {
public:
int minArray(vector<int>& numbers) {
// 指向数组的两端
int i = 0;
int j = numbers.size() - 1;
while(i < j) {
int m = (i + j) / 2;
// 旋转点在右边
if(numbers[m] > numbers[j])
i = m + 1;
// 旋转点在左边
else if(numbers[m] < numbers[j])
j = m;
// 无法判断,缩小范围
else
j--;
}
// 返回旋转点的值
return numbers[i];
}
};思路:
12. 矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false提示:
1 <= board.length <= 200
1 <= board[i].length <= 200代码:
class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
rows = board.size();
cols = board[0].size();
for(int i = 0; i < rows; i++) {
for(int j = 0; j < cols; j++) {
if(dfs(board, word, i, j, 0))
return true;
}
}
return false;
}
private:
int rows, cols;
bool dfs(vector<vector<char>>& board, string word, int i, int j, int k) {
// k: 当前目标字符在word中的索引
// 终止条件
if(i >= rows || i < 0 || j >= cols || j < 0 || board[i][j] != word[k])
return false;
if(k == word.size() - 1)
return true;
// 标记矩阵已访问
board[i][j] = '\0';
bool res = dfs(board, word, i + 1, j, k + 1) ||
dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) ||
dfs(board, word, i, j - 1, k + 1);
// 还原矩阵
board[i][j] = word[k];
return res;
}
};思路:
- 深度优先搜索: 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜到底,再回溯至上个节点,沿另一个方向搜索,以此类推。
- 剪枝: 在搜索中,遇到
这条路不可能和目标字符串匹配成功的情况(例如:此矩阵元素和目标字符不同、此元素已被访问),则应立即返回,称之为可行性剪枝。
13. 机器人的运动范围
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3示例 2:
输入:m = 3, n = 1, k = 0
输出:1提示:
1 <= n,m <= 100
0 <= k <= 20代码:
DFS
class Solution {
public:
int movingCount(int m, int n, int k) {
vector<vector<bool>> visited(m, vector<bool>(n, 0));
return dfs(0, 0, 0, 0, visited, m, n, k);
}
private:
int dfs(int i, int j, int si, int sj, vector<vector<bool>> &visited, int m, int n, int k) {
if(i >= m || j >= n || k < si + sj || visited[i][j])
return false;
visited[i][j] = true;
return 1 + dfs(i + 1, j, (i + 1) % 10 != 0? si + 1: si - 8, sj, visited, m, n, k) +
dfs(i, j + 1, si, (j + 1) % 10 != 0? sj + 1: sj - 8, visited, m, n, k);
}
};BFS
class Solution {
public:
int movingCount(int m, int n, int k) {
vector<vector<bool>> visited(m, vector<bool>(n, 0));
int res = 0;
queue<vector<int>> que;
que.push({0, 0, 0, 0});
while(que.size() > 0) {
vector<int> x = que.front();
que.pop();
int i = x[0], j = x[1], si = x[2], sj = x[3];
if(i >= m || j >= n || k < si + sj || visited[i][j])
continue;
visited[i][j] = true;
res++;
que.push({i + 1, j, (i + 1) % 10 != 0? si + 1: si - 8, sj});
que.push({i, j + 1, si, (j + 1) % 10 != 0? sj + 1: sj - 8});
}
return res;
}
};思路:
14- I. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36提示:
2 <= n <= 58代码:
class Solution {
public:
int cuttingRope(int n) {
if(n <= 3)
return n - 1;
int a = n / 3;
int b = n % 3;
if(b == 0)
return pow(3, a);
if(b == 1)
return pow(3, a - 1) * 4;
return pow(3, a) * 2;
}
};思路:
数学证明方法。
14- II. 剪绳子 II
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]*k[1]*...*k[m - 1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36提示:
2 <= n <= 1000代码:
class Solution {
public:
int cuttingRope(int n) {
if(n <= 3) return n - 1;
int b = n % 3, p = 1000000007;
long rem = 1, x = 3;
for(int a = n / 3 - 1; a > 0; a /= 2) {
if(a % 2 == 1)
rem = rem * x % p;
x = x * x % p;
}
if(b == 0) return rem * 3 % p;
if(b == 1) return rem * 4 % p;
return rem * 6 % p;
}
};15. 二进制中1的个数
请实现一个函数,输入一个整数(以二进制串形式),输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。示例 2:
输入:00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。示例 3:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。提示:
输入必须是长度为 32 的 二进制串 。代码:
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while(n != 0) {
res += n & 1;
n >>= 1;
}
return res;
}
};16. 数值的整数次方
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,$x^n$)。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000示例 2:
输入:x = 2.10000, n = 3
输出:9.26100示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25提示:
-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104代码:
class Solution {
public:
double myPow(double x, int n) {
if(x < 1e-7 && x > -1e-7)
return 0;
long long a = n;
double res = 1;
if(a < 0) {
x = 1 / x;
a = -a;
}
while(a != 0) {
if((a & 1) == 1)
res *= x;
x *= x;
a >>= 1;
}
return res;
}
};17. 打印从1到最大的n位数
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
示例 1:
输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]说明:
用返回一个整数列表来代替打印
n 为正整数代码:
很简单直接的方法,不考虑大数:
class Solution {
public:
vector<int> printNumbers(int n) {
vector<int> res;
int max = 1;
while(n != 0) {
max *= 10;
--n;
}
for(int i = 1; i < max; ++i)
res.push_back(i);
return res;
}
};考虑大数情况:
class Solution {
private:
vector<int> nums;
string s;
public:
vector<int> printNumbers(int n) {
s.resize(n, '0');
dfs(n, 0);
return nums;
}
void dfs(int end, int index) {
if(index == end) {
save();
return;
}
for(int i = 0; i < 10; ++i) {
s[index] = i + '0';
dfs(end, index + 1);
}
}
void save() {
int ptr = 0;
while(ptr < s.size() && s[ptr] == '0')
ptr++;
if(ptr != s.size())
nums.emplace_back(stoi(s.substr(ptr)));
}
};18. 删除链表的节点
给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
返回删除后的链表的头节点。
注意: 此题对比原题有改动
示例 1:
输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.示例 2:
输入: head = [4,5,1,9], val = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.说明:
题目保证链表中节点的值互不相同
若使用 C 或 C++ 语言,你不需要 free 或 delete 被删除的节点代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
if(head->val == val)
return head->next;
ListNode *pre = head, *cur = head->next;
while(cur != nullptr && cur->val != val) {
pre = cur;
cur = cur->next;
}
if(cur != nullptr)
pre->next = cur->next;
return head;
}
};19. 正则表达式匹配
请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符,而'*'表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"ab*ac*a"匹配,但与"aa.a"和"ab*a"均不匹配。
示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。示例 2:
输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false提示:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母以及字符 . 和 *,无连续的 '*'。代码:
21. 调整数组顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
示例:
输入:nums = [1,2,3,4]
输出:[1,3,2,4]
注:[3,1,2,4] 也是正确的答案之一。提示:
0 <= nums.length <= 50000
1 <= nums[i] <= 10000代码:
简单数组组合:
class Solution {
public:
vector<int> exchange(vector<int>& nums) {
vector<int> res;
vector<int> odd;
vector<int> even;
for(int i: nums) {
if(i % 2 == 1) {
odd.push_back(i);
}else {
even.push_back(i);
}
}
res.insert(res.end(), odd.begin(), odd.end());
res.insert(res.end(), even.begin(), even.end());
return res;
}
};双指针:
class Solution {
public:
vector<int> exchange(vector<int>& nums) {
int i = 0, j = nums.size() - 1;
while(i < j) {
// 奇数
while(i < j && (nums[i] & 1) == 1)
i++;
// 偶数
while(i < j && (nums[j] & 1) == 0)
j--;
swap(nums[i], nums[j]);
}
return nums;
}
};22. 链表中倒数第k个节点
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
示例:
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* getKthFromEnd(ListNode* head, int k) {
ListNode *latter = head;
ListNode *former = head;
int cnt = 0;
while(former != nullptr) {
if(cnt == k){
break;
}
cnt++;
former = former->next;
}
while(former != nullptr) {
former = former->next;
latter = latter->next;
}
return latter;
}
};24. 反转链表
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL限制:
0 <= 节点个数 <= 5000代码:
双指针:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode *pre = nullptr, *cur = head, *tmp;
while(cur != nullptr) {
tmp = cur->next;
cur->next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
};双指针:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
return recur(head, nullptr);
}
private:
ListNode* recur(ListNode* cur, ListNode* pre) {
if(cur == nullptr)
return pre;
ListNode* res = recur(cur->next, cur);
cur->next = pre;
return res;
}
};25. 合并两个排序的链表
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
示例1:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4限制:
0 <= 链表长度 <= 1000代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode *dum = new ListNode(0), *cur = dum;
while(l1 != nullptr && l2 != nullptr) {
if(l1->val < l2->val) {
cur->next = l1;
l1 = l1->next;
}else {
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
cur->next = l1 != nullptr? l1: l2;
return dum->next;
}
};26. 树的子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2给定的树 B:
4
/
1返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true限制:
0 <= 节点个数 <= 10000代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
return (A != nullptr && B != nullptr) &&
(recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
}
bool recur(TreeNode* A, TreeNode* B) {
if(B == nullptr)
return true;
if(A == nullptr || A->val != B->val)
return false;
return recur(A->left, B->left) && recur(A->right, B->right);
}
};27. 二叉树的镜像
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/ \
2 7
/ \ / \
1 3 6 9镜像输出:
4
/ \
7 2
/ \ / \
9 6 3 1
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]限制:
0 <= 节点个数 <= 1000代码:
递归:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(root == nullptr)
return nullptr;
TreeNode* tmp = root->left;
root->left = mirrorTree(root->right);
root->right = mirrorTree(tmp);
return root;
}
};辅助栈(队列):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(root == nullptr)
return nullptr;
stack<TreeNode*> stack;
stack.push(root);
while(!stack.empty()) {
TreeNode* node = stack.top();
stack.pop();
if(node->left != nullptr)
stack.push(node->left);
if(node->right != nullptr)
stack.push(node->right);
TreeNode* tmp = node->left;
node->left = node->right;
node->right = tmp;
}
return root;
}
};28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false限制:
0 <= 节点个数 <= 1000代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return root == nullptr? true: recur(root->left, root->right);
}
private:
bool recur(TreeNode* L, TreeNode* R) {
if(L == nullptr && R == nullptr)
return true;
if(L == nullptr || R == nullptr || L->val != R->val)
return false;
return recur(L->left, R->right) && recur(L->right, R->left);
}
};29. 顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]限制:
0 <= matrix.length <= 100
0 <= matrix[i].length <= 100代码:
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
if(matrix.empty())
return res;
int l = 0;
int r = matrix[0].size() - 1;
int t = 0;
int b = matrix.size() - 1;
while(true) {
// ->
for(int i = l; i <= r; i++)
res.push_back(matrix[t][i]);
if(++t > b)
break;
// |>
for(int i = t; i <= b; i++)
res.push_back(matrix[i][r]);
if(--r < l)
break;
// <-
for(int i = r; i >= l; i--)
res.push_back(matrix[b][i]);
if(--b < t)
break;
// >|
for(int i = b; i >= t; i--)
res.push_back(matrix[i][l]);
if(++l > r)
break;
}
return res;
}
};30. 包含min函数的栈
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.提示:
各函数的调用总次数不超过 20000 次代码:
class MinStack {
public:
stack<int> A, B;
/** initialize your data structure here. */
MinStack() {
B.push(INT_MAX);
}
void push(int x) {
A.push(x);
B.push(::min(B.top(), x));
}
void pop() {
A.pop();
B.pop();
}
int top() {
return A.top();
}
int min() {
return B.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(x);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->min();
*/31. 栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。提示:
0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed 是 popped 的排列。代码:
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
vector<int> vec;
int i = 0;
for(int num: pushed) {
vec.push_back(num);
while(!vec.empty() && vec.back() == popped[i]) {
vec.pop_back();
++i;
}
}
return vec.empty();
}
};32 - I. 从上到下打印二叉树
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回:
[3,9,20,15,7]提示:
节点总数 <= 1000代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
vector<int> res;
if(!root)
return res;
queue<TreeNode*> q;
q.push(root);
while(q.size()) {
TreeNode* node = q.front();
q.pop();
res.push_back(node->val);
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
return res;
}
};32 - II. 从上到下打印二叉树 II
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]提示:
节点总数 <= 1000代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if(!root)
return {};
vector<vector<int>> res;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int len = que.size();
vector<int> level;
while(len) {
TreeNode* node = que.front();
if(node->left)
que.push(node->left);
if(node->right)
que.push(node->right);
level.push_back(node->val);
que.pop();
len--;
}
res.push_back(level);
}
return res;
}
};版权属于:moluuser
本文链接:https://archive.moluuser.com/archives/81/
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。


